OmniQuant: Omnidirectionally Calibrated Quantization for Large Language Models

文章目录

1. 1. 介绍
2. 2. 方法
   1. 2.1. 分块量化
   2. 2.2. LWC (Learnable Weight Clipping)
   3. 2.3. LET (Learnable Equivalent Transformation)
      1. 2.3.1. Linear
      2. 2.3.2. Attention operation
3. 3. 实验
4. 4. 代码
5. 5. 参考资料

介绍

很多针对LLM的PTQ量化算法在设计参数的时候都添加了太多的先验知识，导致性能不佳，尤其在低比特量化中。为了解决这个问题，本文提出了全向校准量化（OmniQuant）技术。

OmniQuant包含两个组件，可学习权重裁剪 (LWC) 和可学习等效变换 (LET)。 LWC通过优化限幅阈值来调节权重的极值。同时，LET 通过将量化的挑战从激活转移到权重来解决激活异常值。OmniQuant 在使用逐块误差最小化的可微框架内运行。在校准的时候，OmniQuant 冻结了模型原始的全精度权重，仅包含LWC和LET可学习的量化参数。

本文也利用了 LLM.int8()和 AWQ中的几个结论：

• 相比模型的权重，大模型的激活的异常值（绝对值远超别的参数）的绝对值更大。并且无论是哪个 token或者哪个 Layer，异常值都集中在固定的少数维度。
• 由于与激活相对应的权重的重要性，权重的量化误差在最终性能中也起着关键作用。

方法

分块量化

和别的针对LLm的PTQ量化方法一样，为了降低LLM量化的复杂度，OmniQuant也是逐个block进行量化的。针对每个block，优化的目标函数为：

\[ \arg \min_{\Theta_1, \Theta_2} \left\| \mathcal{F}(\mathbf{W}, \mathbf{X}) - \mathcal{F} \left( Q_w(\mathbf{W}; \Theta_1, \Theta_2), Q_a(\mathbf{X}, \Theta_2) \right) \right\| \]

其中，\(\mathcal{F}\) 表示 LLM 中一个 Transformer 块的映射函数，\(\mathbf{W}\) 和 \(\mathbf{X}\) 分别是全精度的权重和激活，\(Q_w(\cdot)\) 和 \(Q_a(\cdot)\) 分别表示权重和激活的量化器，\(\Theta_1\) 和 \(\Theta_2\) 分别是可学习权重裁剪（LWC）和可学习等效变换（LET）的量化参数。公式中的逐块量化在移动到下一个块之前，依次量化一个 Transformer 块的参数。

以block作为量化优化的最小单位有两个好处：

• 可以对LWC和LET的参数同时进行训练
• 可以显著减少资源需求

LWC (Learnable Weight Clipping)

LWC考虑在量化函数里面加入可学习的参数，具体来说，LWC 优化了一个Clip过程，其公式如下：

\[ \mathbf{W}_q = \text{clamp}\left(\left\lfloor \frac{\mathbf{W}}{h} \right\rceil + z, 0, 2^N - 1\right), \quad \text{其中 } h = \frac{\gamma \max(\mathbf{W}) - \beta \min(\mathbf{W})}{2^N - 1}, \quad z = -\left\lfloor \frac{\beta \min(\mathbf{W})}{h} \right\rceil \]

公式里面的\(\left\lfloor \cdot \right\rceil\)代表取整操作，\(N\)是量化的比特数，\(\mathbf{W}_q\) 和 \(\mathbf{W}\) 分别表示量化后的权重和全精度权重。\(h\) 是权重的归一化因子，\(z\) 是零点值。clamp 操作将值限制在 \(N\) 位整数范围内，具体为 \([0, 2^N - 1]\)。在公式中，\(\gamma \in [0, 1]\) 和 \(\beta \in [0, 1]\) 是分别针对权重上界和下界的可学习剪辑强度。我们通过 sigmoid 函数对 \(\gamma\) 和 \(\beta\) 进行初始化。因此，在公式 (1) 中，\(\Theta_1 = \{\gamma, \beta\}\)。

其中\(h,z\)是个整型，如果直接学习可能难度较大。

LET (Learnable Equivalent Transformation)

考虑到激活中的异常值是系统性的并且对于特定通道是固定的，follow之前的工作，使用通道级缩放和通道级移位来操纵激活分布。参数方面作者认为之前的工作是手动设计的参数，导致结果可能不是很理想。

OmniQuant 没有引入额外的计算或参数，因为和AWQ量化算法一样，LWC 中的限幅阈值和 LET 中的等效因子可以融合为量化权重。

Linear

线性层接受一个输入标记序列 \(\mathbf{X} \in \mathbb{R}^{T \times C_\text{in}}\)，其中 \(T\) 是标记长度，其操作是权重矩阵 \(\mathbf{W} \in \mathbb{R}^{C_\text{in} \times C_\text{out}}\) 与偏置向量 \(\mathbf{B} \in \mathbb{R}^{1 \times C_\text{out}}\) 的乘积。一个数学等价的线性层表示为：

\[ \mathbf{Y} = \mathbf{X} \mathbf{W} + \mathbf{B} = \underbrace{\left(\mathbf{X} - \delta\right) \odot s}_{\tilde{\mathbf{X}}} \cdot \underbrace{\left(s \odot \mathbf{W}\right)}_{\tilde{\mathbf{W}}} + \underbrace{\left(\mathbf{B} + \delta \mathbf{W}\right)}_{\tilde{\mathbf{B}}} \]

其中，\(\mathbf{Y}\) 表示输出，\(s \in \mathbb{R}^{1 \times C_\text{in}}\) 和 \(\delta \in \mathbb{R}^{1 \times C_\text{in}}\) 分别是通道级的缩放和偏移参数。\(\tilde{\mathbf{X}}\)，\(\tilde{\mathbf{W}}\) 和 \(\tilde{\mathbf{B}}\) 分别是等效的激活、权重和偏置，符号“\(\odot\)”表示元素级的除法和乘法。

通过公式，激活被转化为量化友好的形式，但代价是增加了权重量化的难度。在此意义上，LWC可以改善通过 LET 实现的权重-激活量化的性能，因为它使权重更加量化友好。最终，我们对转换后的激活和权重进行量化，公式如下：

\[ \mathbf{Y} = Q_a(\tilde{\mathbf{X}}) Q_w(\tilde{\mathbf{W}}) + \tilde{\mathbf{B}} \]

其中，\(Q_a\) 是普通的 MinMax 量化器，\(Q_w\) 是带有可学习权重剪辑（即 LWC）的 MinMax 量化器。

请注意，\(\tilde{\mathbf{X}}\) 中的缩放和偏移参数可以吸收进前面的归一化或线性层，而 \(\tilde{\mathbf{W}}\) 中的缩放因子可以融合进原始线性权重 \(\mathbf{W}\) 中。因此，公式中的等效变换可以在不引入额外参数或成本的情况下有效减少量化误差。

OmniQuant在 LLM 的线性层（除了 FFN 的第二个线性层）中使用此等效变换。这可能是因为在应用可学习的等效变换时，非线性层后的特征高度稀疏，导致梯度不稳定。

Attention operation

除了线性层外，注意力操作也占据了计算的一个重要部分。此外，LLM 的自回归模式需要存储每个标记的键值（KV）缓存，这对于长序列带来了大量的内存需求。因此，考虑把\(Q,K,V\)矩阵在权重-激活量化设置中量化为低比特值。具体而言，自注意力相似度矩阵的可学习等效变换可写为：

\[ \mathbf{P} = \text{Softmax}(\mathbf{Q} \mathbf{K}^T) = \text{Softmax} \left( \underbrace{\mathbf{Q} \odot s_a}_{\tilde{\mathbf{Q}}} \, \underbrace{(s_a \odot \mathbf{K}^T)}_{\tilde{\mathbf{K}}^T} \right). \]

其中，\(s_a \in \mathbb{R}^{1 \times C_\text{out}}\) 是相似度矩阵中的缩放因子。量化的相似度矩阵计算表示为 \(\mathbf{P} = \text{Softmax}(Q_a(\tilde{\mathbf{Q}}) Q_a(\tilde{\mathbf{K}}^T))\)。这里我们同样使用 MinMax 量化方案 \(Q_a\) 对 \(\tilde{\mathbf{Q}}/\tilde{\mathbf{K}}\) 矩阵进行量化。我们可以得出 \(\Theta_2 = \{ \delta, s, s_a \}\) 。

\(\tilde{\mathbf{Q}}\) 和 \(\tilde{\mathbf{K}}\) 中的通道级缩放因子，可以分别吸收到查询和键投影的线性权重中。值得一提的是，由于逆变换操作的存在，输出投影线性层中的显式变换在其分布上已按通道维度进行了更改，因此省略了 \(\mathbf{V}\) 的变换。

实验

首先测试了只量化模型权重的结果，和GPTQ和AWQ进行了对比，取得了在WikiText2上最低的困惑度。

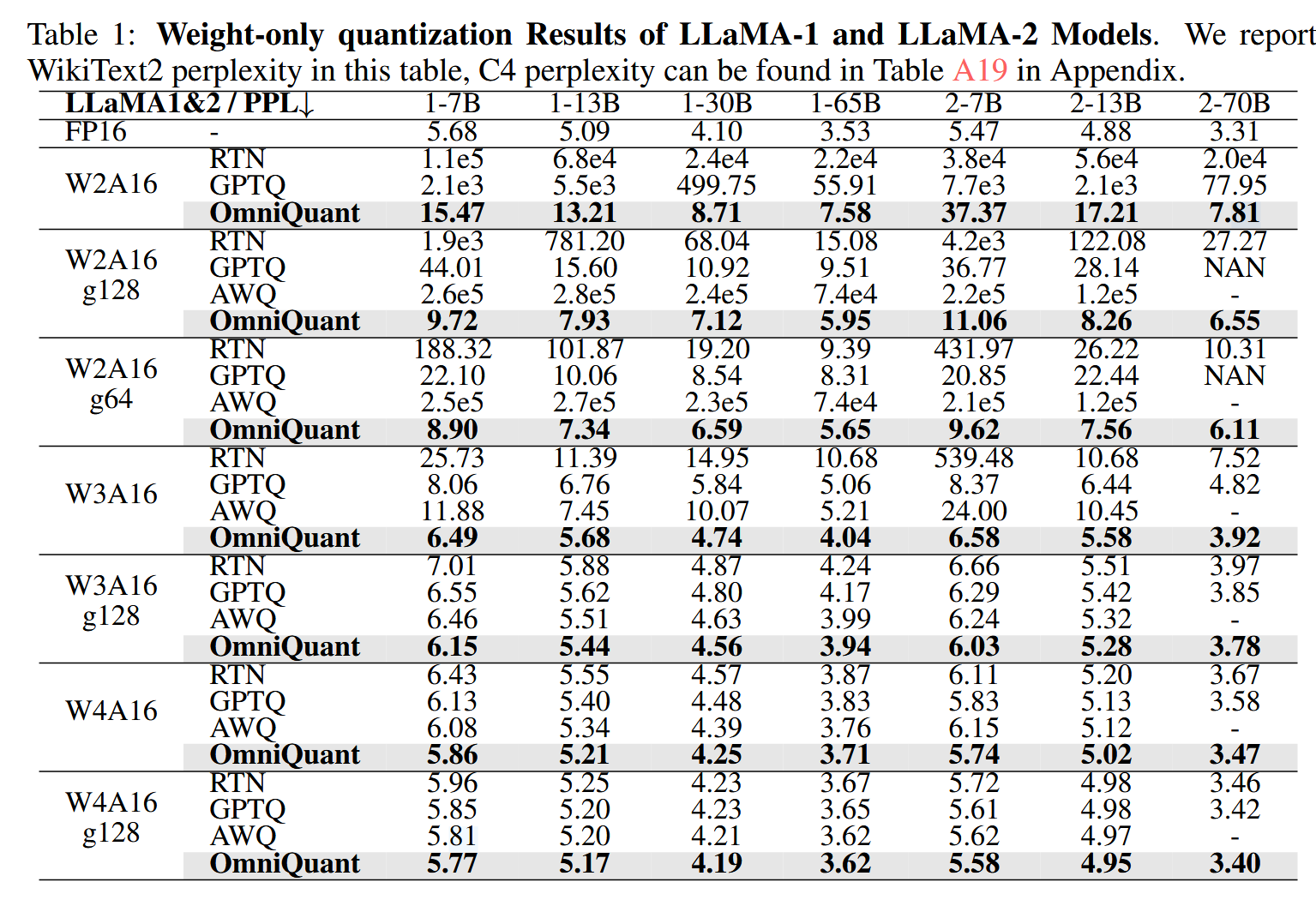
也测试了权重和激活都进行量化的表现，对比的baseline是SmoothQuant和LLM-QAT，可以看到甚至比LLM-QAT这种QAT量化方法还要好。

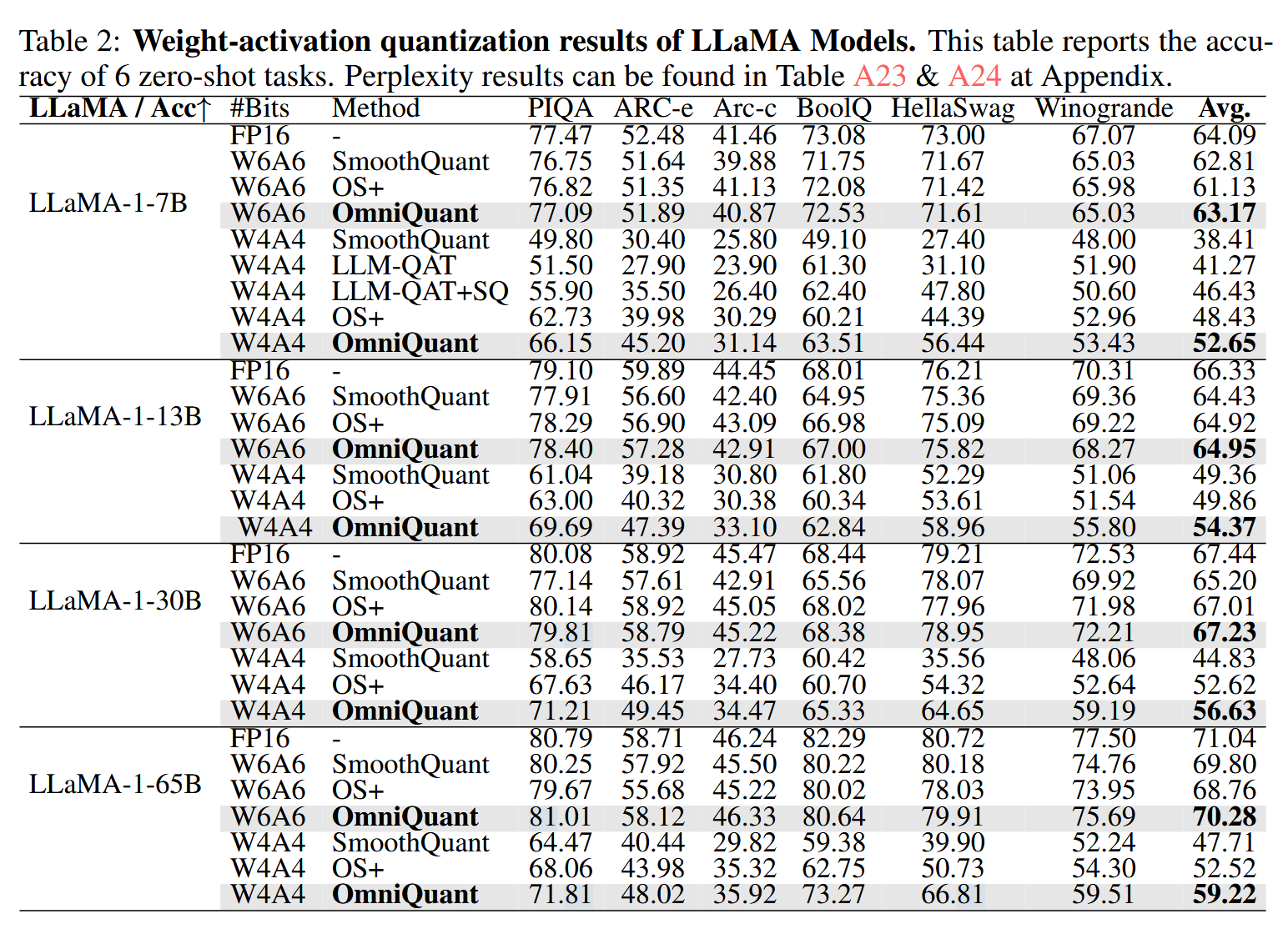
然后还参考AWQ的论文，测试了模型回答问题的准确率。把两个模型的回答连接在一起，让GPT-4判断哪个回答更好，为了去除顺序的影响，会交换顺序让GPT-4再回答一次，结果如下图所示：

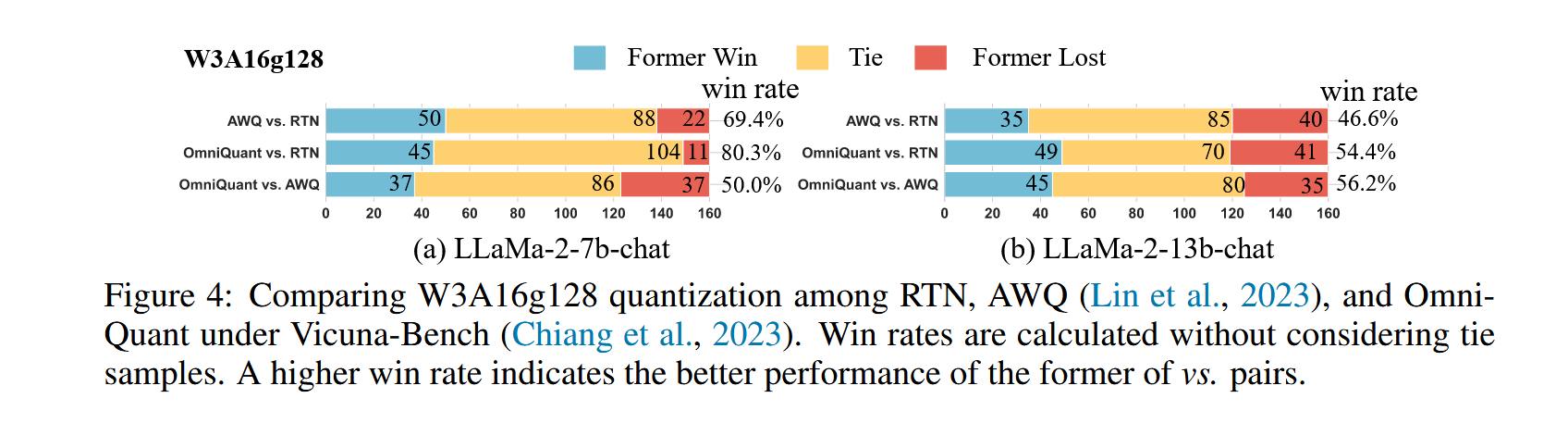
最后测试了模型的效率情况，统计了算法在不同规模的Llama上的存储需求和推理速度。

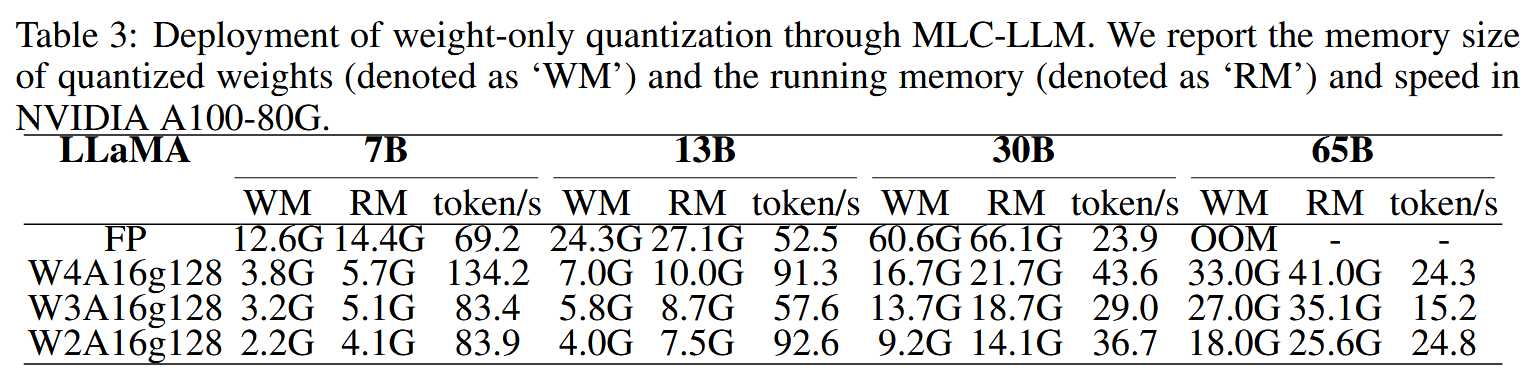
这篇论文的附录罗列了很多细节，需要的可以去看原文。

代码

论文源码：OpenGVLab/OmniQuant: [ICLR2024 spotlight] OmniQuant is a simple and powerful quantization technique for LLMs.

参考资料

• [2308.13137] OmniQuant: Omnidirectionally Calibrated Quantization for Large Language Models
• OpenGVLab/OmniQuant: [ICLR2024 spotlight] OmniQuant is a simple and powerful quantization technique for LLMs.