摘要
这篇论文展示了BitNet,一种为大型语言模型设计的可扩展和稳定的1-bit转换器架构。具体地说,引入了BitLinear作为nn.Linar的插入替代,以便从头开始训练1-bit的权重。在语言建模上的实验结果表明,与最先进的8-bit量化方法和FP16 Transformer相比,BitNet在显著降低内存占用和能量消耗的同时,实现了强力的性能。此外,BitNet还展示了一种类似于全精度Transformers的scaling low,这表明它可以在保持效率和性能效益的同时有效地扩展到更大的语言模型。
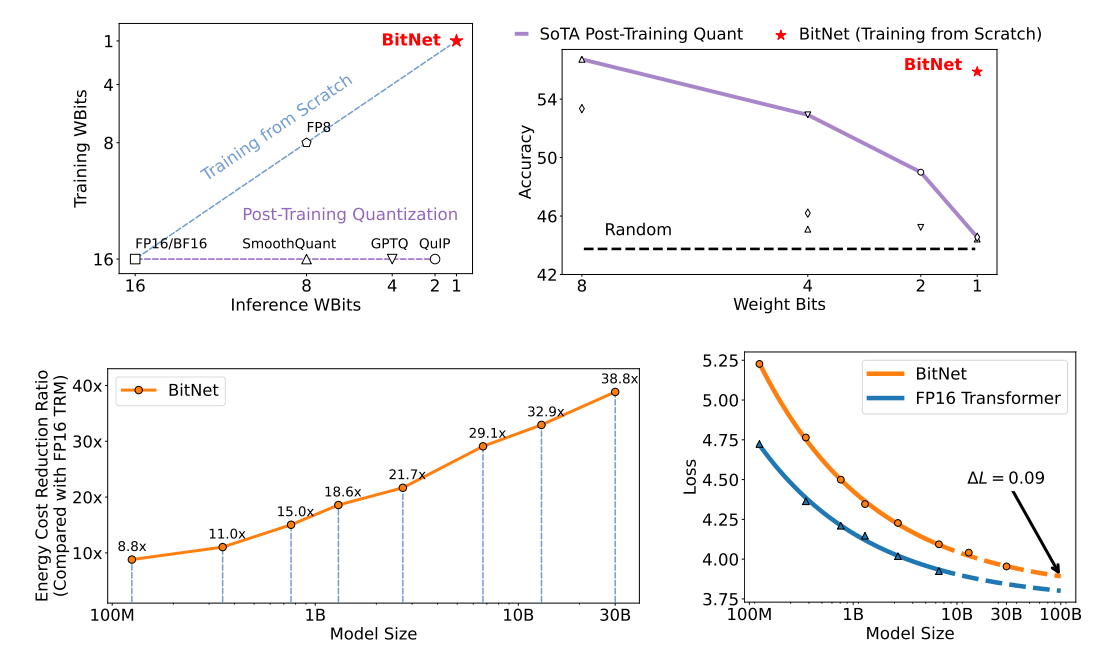
图1: BitNet从头开始训练1-bit Transformers,以一种高效的方式获得竞争结果。BitNet明显优于最先进的量化方法。随着模型规模的扩大,成本节约变得更加显著,同时实现与FP16训练的模型的竞争性能。
介绍
大模型的推理陈本较高,一个降低成本的重要办法就是量化。
目前LLM的量化方法大多数都是训练后量化PTQ,成本比QAT低但在极低精度表现不好。
LLM量化的另一类方法是量化感知训练QAT,效果更好,但是在低精度下难以收敛。此外,不确定QAT是否遵循scaling low。
本文首次提出1-bit大模型QAT,提出BitNet,LLM的1-bit transformer。采用低精度二进制权重和量化激活,同时在训练期间保持优化器状态和梯度的高精度。BitNet 架构的实现非常简单,只需要替换Transformer 中的线性投影(即 PyTorch 中的 nn.Linear)。
在一系列语言建模基准上评测了BitNet。与最先进的量化方法和fp16的baseline相比有竞争力。有效减少了内存占用和能耗。同时遵循类似的scaling low。
BitNet
模型整体架构图如图所示:
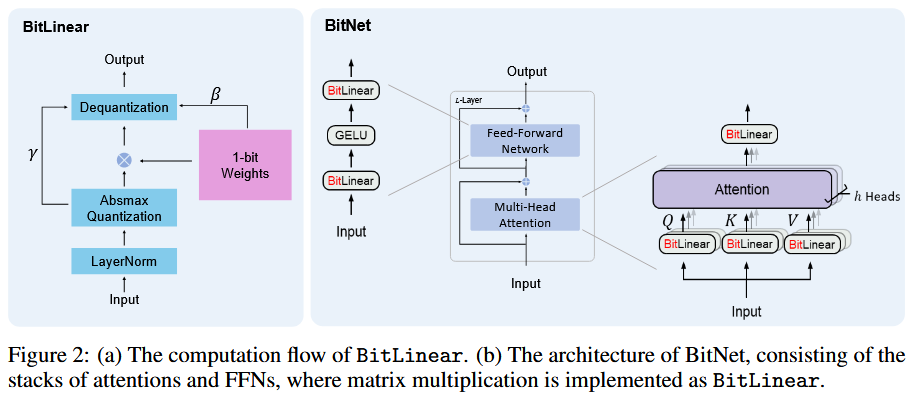
相比transformer,使用BitLinear替代原有的Linear和传统的矩阵乘法,其他组件保持高精度,作者认为原因如下:
- 残差连接和层归一化对大型语言模型的计算成本可以忽略不计
- 随着模型变大,QKV 变换的计算成本比参数投影小得多
- 保留输入/输出嵌入的精度,因为语言模型必须使用高精度概率来执行采样
BitLinear
BitLinear把权重二值化为+1或-1。在训练的时候,为了保证反向传播的有效性,模型的参数 $ W ^{n m} $是保持高精度的,但是forward的时候会进行量化操作:
\[ \tilde{W} = \text{Sign}(W - \alpha), \quad \text{Sign}(W_{ij}) = \begin{cases} +1, & \text{if } W_{ij} > 0, \\ -1, & \text{if } W_{ij} \leq 0, \end{cases} \quad \alpha = \frac{1}{nm} \sum_{ij} W_{ij} \]
激活也会量化到$[-Q_{b},Q_{b}] (Q_{b}=2^{b-1}) $,同时添加细致扰动防止clip时溢出:
\[ \tilde{x} = \text{Quant}(x) = \text{Clip}\left( x \times \frac{Q_b}{\gamma}, -Q_b + \epsilon, Q_b - \epsilon \right) \\ \text{Clip}(x, a, b) = \max(a, \min(b, x)), \quad \gamma = \lVert x \rVert_{\infty} \]
对于非线性函数之前的激活,会缩放到\([0,Q_{b}] (Q_{b}=2^{b-1})\):
\[ \tilde{x} = \text{Quant}(x) = \text{Clip}\left( (x - \eta) \times \frac{Q_b}{\gamma}, \epsilon, Q_b - \epsilon \right), \quad \eta = \min_{ij} x_{ij} \]
其中BitLinear的forward过程为:
\[ \\ \text{LN}(x) = \frac{x - E(x)}{\sqrt{\text{Var}(x)} + \epsilon}, \quad \beta = \frac{1}{nm} \lVert W \rVert_1 \\ y = \tilde{W} \tilde{x} = \tilde{W} \, \text{Quant}(\text{LN}(x)) \times \frac{\beta \gamma}{Q_b} \]
下面这段分析我也不是很理解,一直不知道约等于是怎么来的?
分析:
\[ \begin{align*} y &= \tilde{W} \tilde{x} \ ,\\ \text{Var}(y) &= n \, \text{Var}(\tilde{w} \tilde{x}) \\ \quad &= n E[\tilde{w}^2] E[\tilde{x}^2] \\ \quad &= n \beta^2 E[\tilde{x}^2] \approx E[\tilde{x}^2] \end{align*} \]
当使用归一化操作后,\(Var(y) ≈ E[LN( \tilde{x} )^2] = 1\)
同时,为了支持张量并行(一个张量拆分到多卡上),部分参数的需要通过
all-reduce来确定,但是会增加通信成本,因此考虑分组确定,即将权重和激活分为几组,然后独立估计每组的参数:
\[ \alpha_g = \frac{G}{nm} \sum_{ij} W_{ij}^{(g)}, \quad \beta_g = \frac{G}{nm} \lVert W^{(g)} \rVert_1 \]
模型训练
STE
由于有量化操作不可微分,因此考虑引入STE进行梯度的近似。
混合精度
虽然权重和激活被量化为低精度,但梯度和优化器状态以高精度存储,以确保训练的稳定性和准确性。以高精度格式为可学习参数维护一个潜在权重,以累积参数更新。潜在权重在前向传播过程中被动态二值化,并且从不用于推理过程。
增大学习率
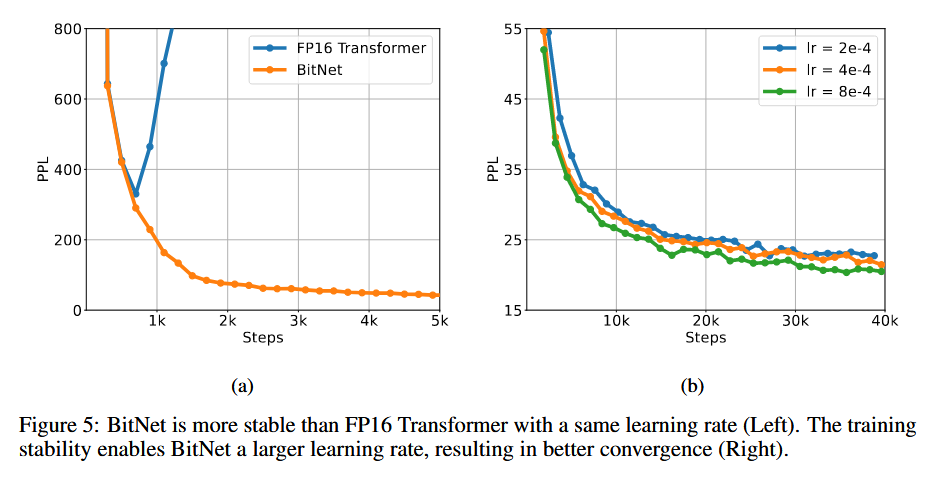
潜在权重的小幅度更新可能不会引起1位权重的变化,为了加速收敛,考虑增大学习率的值。实验表明,BitNet 在收敛方面受益于较大的学习率,而 FP16 Transformer 在相同学习率的训练开始时会发散。
计算能效
论文还给出了理论的计算能效,主要关注矩阵乘法部分。
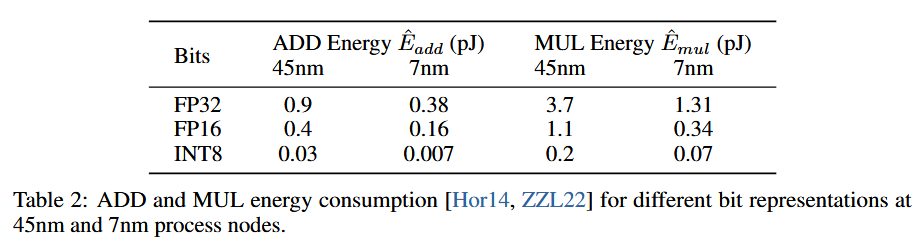
对于transformer里的矩阵乘法,两个矩阵维度分别为\(m \times n\)和\(n \times m\),能效计算公式为:
\[ E_{add} = m \times (n - 1) \times p \times \hat{E}_{add} \\ E_{mul} = m \times n \times p \times \hat{E}_{mul} \]
对于BitNet,矩阵权重为1比特的,因此矩阵乘法的能耗主要由加法决定,和transformer的加法能耗公式相同,而用于放缩的乘法能耗公式为:
\[ E_{mul} = (m \times p + m \times n) \times \hat{E}_{mul} \]
16位transformer对比
使用各种规模的 BitNet 训练一系列自回归语言模型,范围从 125M 到 30B。这些模型在英语语料库上进行训练,该语料库由 Pile 数据集、Common Crawl 快照、RealNews 和 CC-Stories 数据集组成。具体的训练超参可以阅读原文。同时训练作为对比的transformer。
从测试可以发现,模型的loss与transformer相比有类似的scaling low。
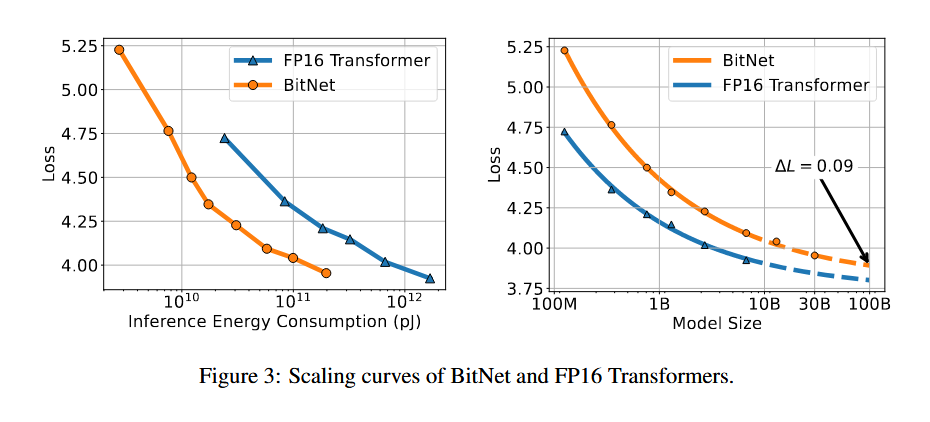
能耗也有类似的规律。
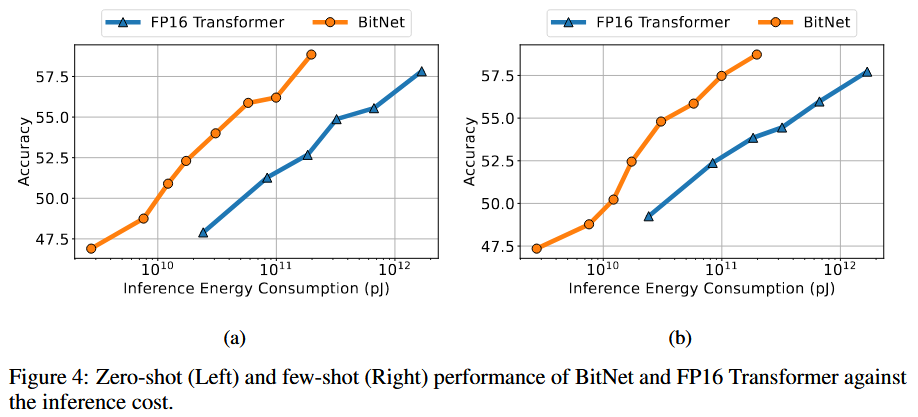
当增大学习率的时候,BitNet可以更好的保持性能。
与PTQ对比
使用与前文相同的设置训练BitNet和transformer,在训练好的transformer上尝试PTQ量化。
结果如下所示:
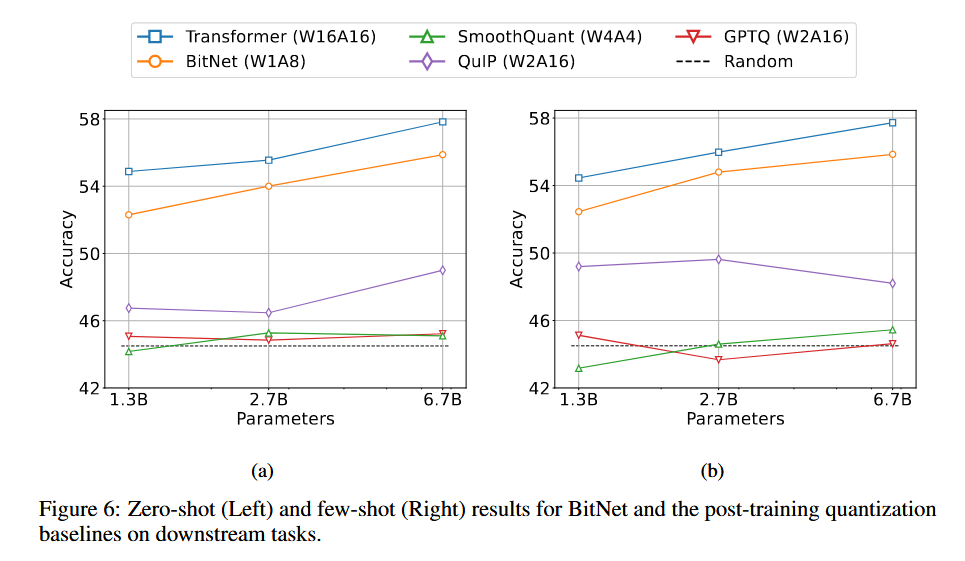
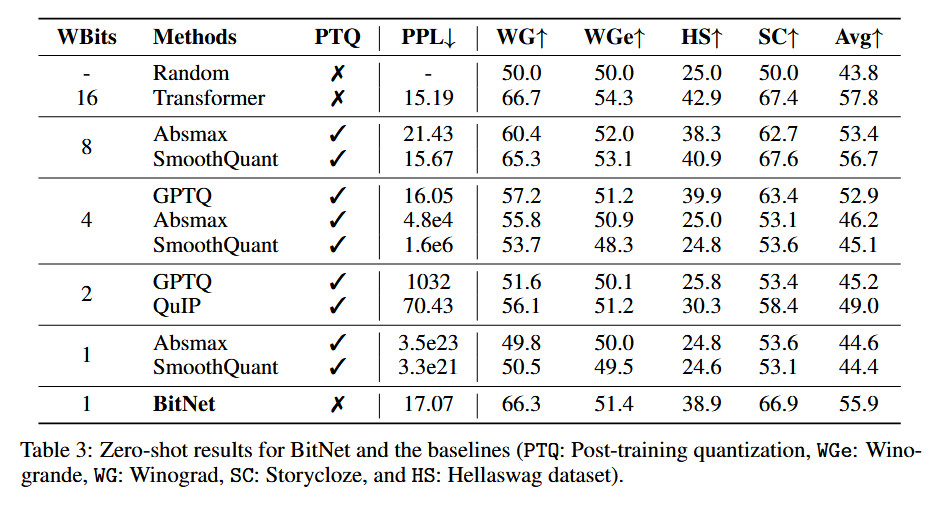
在PPL和Acc上结果明显优于目前最优的PTQ方法。
消融实验
作者还尝试了消融实验:
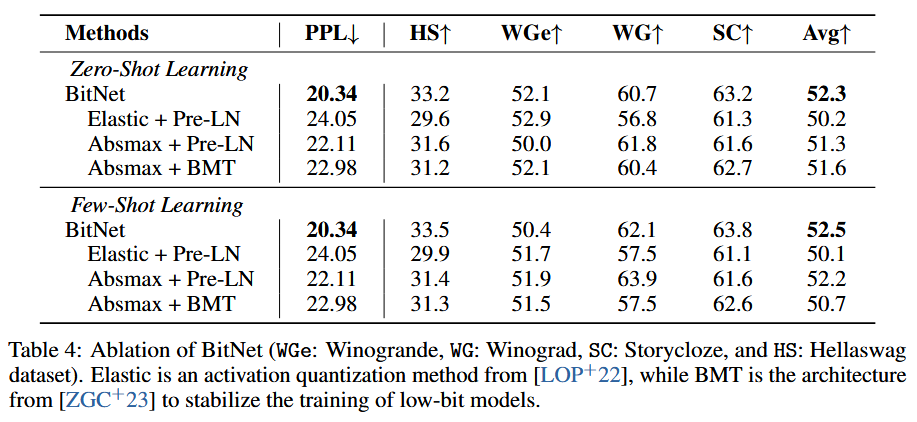
BitNet使用的是
absmax+SubLn。Elastic代表弹性的量化函数,通过可学习的参数动态调整尺度。Pre-LN
是 GPT 相关的默认架构,而 BMT 已被证明可以提高二值化模型的稳定性。
代码
核心代码文件为:BitNet/bitnet/bitlinear.py at main · kyegomez/BitNet



