介绍
传统的词向量是独热编码One-Hot,每个词语对应的向量只有一位为1,其余为0,通过这个1的位置区分向量
Word2Vec是一种Distributed Representation,相比独热编码有以下优点:
- 维度远小于独热编码
- 能更好的反馈向量间的关系
- 每个维度都被充分利用
Word2Vec的网络结构
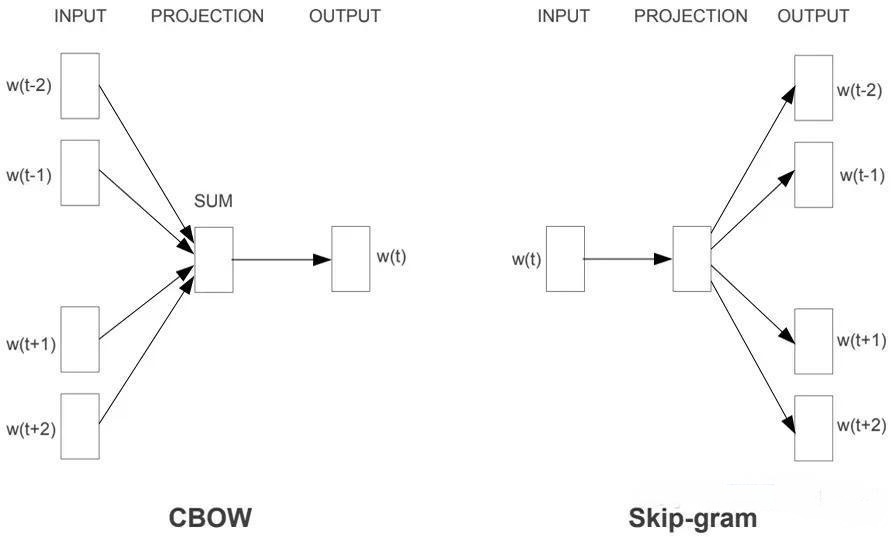
Word2Vec是轻量级的神经网络,其模型仅仅包括输入层、隐藏层和输出层,模型框架根据输入输出的不同,主要包括CBOW和Skip-gram模型。
CBOW模型,在知道上下文的情况下预测中心词\(w_t\)
Skip-gram模型,在知道中心词\(w_t\)的情况下预测
网络结构基础
下图是两种模型结构的基础,是输入一个词,预测一个词
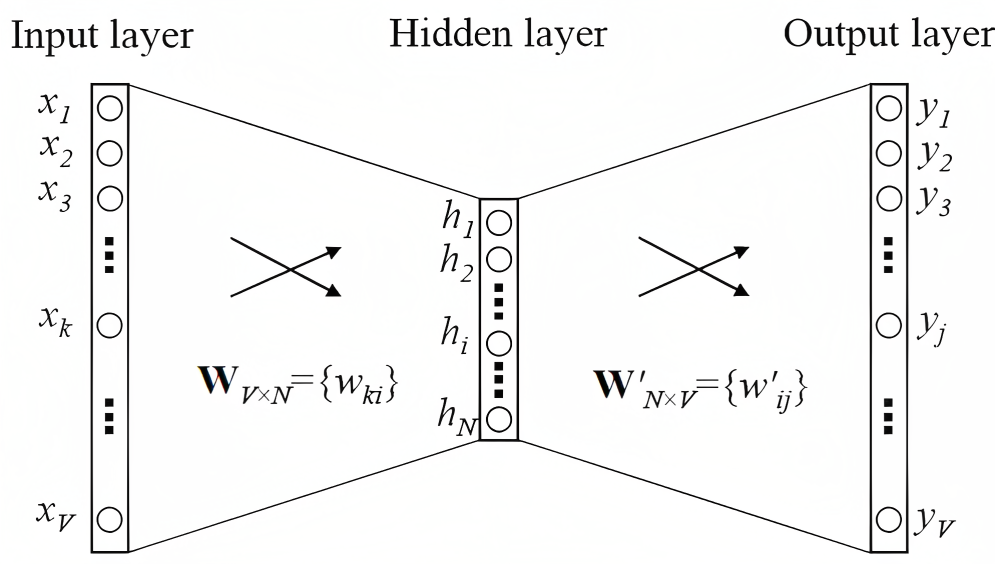
中间的运算都会使用矩阵方便加速:
- 一个词语转换成对应的词向量,就会使用独热编码乘以这个\(W_{V\times N}\),(其中V为词库大小,N为词向量维度数)
- 一个词向量和别的词的上下文向量点乘,也会乘以矩阵\(W^{'}_{V\times N}\),得到\(\bm y\),也就是\(\bm u^T\cdot \bm v\)
之后词语k的概率就是softmax:
\[ P(w_k|w_c)=\frac{\exp(\bm u^T_k\cdot \bm v_c)}{\sum \exp(\bm u^T_i\cdot \bm v_c)}=\frac{\exp(\bm y_k)}{\sum \exp(\bm y_i)} \]
之后就是追求句子概率最大化:
\[ \prod P(w_k|w_c) \]
对数化后取负数就得到了损失函数:
\[ Loss=\sum_{o \in context}( \bm u^T_k\cdot \bm v_c-log(\sum_{i \in V}exp(\bm u^T_i\cdot \bm v_c))) \]
通过微分,我们可以获得其相对于中心词向量\(\bm v_c\)的梯度为

其他向量的方法也是类似.这里就不给予推导.
CBOW 词袋模型
用上下文预测中心词\(w_t\)

Skip-gram Model 跳元模型
用中心词\(w_t\)预测上下文

近似训练
由于softmax操作的性质,上下文词可以是词表V中的任意项,式子包含与整个词表大小一样多的项的求 和。因此,跳元模型的梯度计算和连续词袋模型的梯度计算都包含求和。不幸的是, 在一个词典上(通常有几十万或数百万个单词)求和的梯度的计算成本是巨大的!
为了降低上述计算复杂度,引入两种近似训练方法:负采样和分层softmax。由于跳元模型和连续词袋 模型的相似性,将以跳元模型为例来描述这两种近似训练方法。
负采样Negative Sampling
负采样指的是加入一些负样本来进行模型的训练.
负采样修改了原目标函数来减少运算成本.
给定中心词\(w_c\)的上下文窗口,任意上下文词\(w_o\)来自该上下文窗口的被认为是由下式建模概率的事件:
\[ P(D=1|w_c,w_o)=\sigma(\bm u^T_o\bm v_c) \]
其中
\[ \sigma(x)=\frac{1}{1+exp(-x)} \]
考虑最大化联合概率
\[ \prod^T_{t=1}\prod_{-m\leqslant j \leqslant m,j\neq 0} P(D=1|w_t,w_{t+j}) \]
然而这样只考虑了正样本,当且仅当所有词向量都等于无穷大的时候,这个式子会最大化为1,因此考虑加入一些噪声词作为负样本.
\[ \prod^T_{t=1}\prod_{-m\leqslant j \leqslant m,j\neq 0} P(w_{t+j}|w_t) \\ 其中 P(w_{t+j}|w_t)=P(D=1|w_t,w_{t+j})\prod^K_{k=1,w_k\thicksim P(w)}P(D=0|w_t,w_k) \]
关于条件概率的对数损失函数为:

分层softmax Hierarchical Softmax
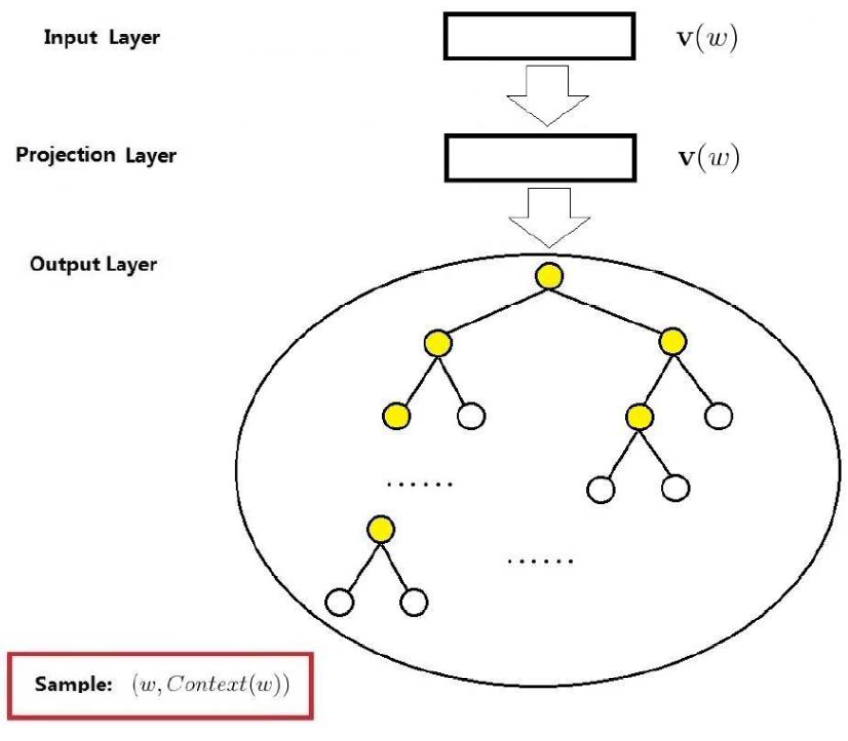
这是一颗二叉树,从根节点开始,每次走左节点还是右节点都是概率时间,每个叶子节点都是词,所以根据中心词向量预测上下文可以看作是从根节点到叶子节点路径的概率乘积.
一种构造二叉树的方法是根据词语的出现频率构造哈夫曼树.
在非叶子节点\(i\)走右边的概率是
\[ \sigma(\bm x^T_w \bm \theta)=\frac{1}{1+eps(-\bm x^T_w \bm \theta)} \]
根据中心词\(w_t\)预测上下文\(w_o\)的概率也很就容易得到.
参考资料
第一篇写的最为详细全面,包括本文各种没有提到的细节,点赞!
参考资料里面第一篇和第三篇其实说的是一个东西,只不过一个是以矩阵的形式给出的.
可以通过奇异值分解减少词的特征维度.



