介绍
求解最优化是一类十分常见且难以求解的问题,因此,考虑开一个博客系统性的介绍一下重要解法:拉格朗日乘数法(Lagrange Multiplier Method)。之后再扩展到广义的拉格朗日乘数法。
拉格朗日乘数法的重点是在一些列约束条件下,构造包含隐藏条件的拉格朗日函数等同于优化的目标函数。
隐藏条件指的是在限制条件和拉格朗日函数共同作用下实际暗含的一些条件或方程。
最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值(因为最小值与最大值可以很容易转化,即最大值问题可以转化成最小值问题) 。
无约束条件
对所有变量求偏导计算极值点后,把极值点代回原函数验证即可。
等式约束条件
求一个函数在等式约束下的最值,即
\[ \begin{aligned} \min & \quad f(\mathbf{x}) \\ \text{s.t.} & \quad h_j(\mathbf{x}) = 0, \quad j = 1, 2, \dots, l \end{aligned} \]
定义拉格朗日函数\(F(x)\),其中\(\lambda_k\)为引入的变量:
\[ F(\mathbf{x}, \lambda) = f(\mathbf{x}) + \sum_{j=1}^{l} \lambda_j h_j(\mathbf{x}) \]
求解极值点只需求解方程组:
\[ \frac{\partial F}{\partial x_i} = 0 \\ \frac{\partial F}{\partial \lambda_j} = 0 \]
下面关于不等式约束下的最优值求解给了通用的证明过程,不过,维基百科列出了一个形象的解释:
考虑有个优化问题:
\[ \begin{aligned} \min & \quad f(x, y) \\ \text{s.t.} & \quad g(x, y) = c \end{aligned} \]
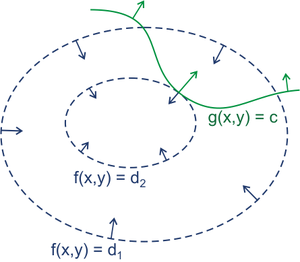
图上画的是两个函数的等高线,箭头表示梯度方向(暂时不考虑梯度正负)。绿色的线是约束条件,代表需要在绿色的线上寻找最优点。最优点显然在两个函数相切的地方,即两个函数梯度共线,\(\nabla f(x, y) = \lambda \left( \nabla g(x, y) - C \right)\)(\(\nabla\)代表梯度算子,\(\lambda\)是非0实数),这就是等式约束下拉格朗日乘数法的隐藏条件。
从反证法考虑,假如两个梯度不共线,那么沿着约束函数的切向,即与约束函数梯度垂直的方向,一定可以找到一个向量,与约束函数梯度垂直且在目标函数梯度上有分量。那么沿着该向量方向修改变量,可以在约束函数值不变的条件下继续优化目标函数。
不等式条件约束
添加上不等式约束条件,就得到了广义拉格朗日问题,此时的最优化问题为,
\[ \begin{aligned} \min & \quad f(\mathbf{\mathbf{x}}) \\ \text{s.t.} & \quad h_j(\mathbf{\mathbf{x}}) = 0, \quad j = 1, 2, \dots, p \\ & \quad g_k(\mathbf{\mathbf{x}}) \leq 0, \quad k = 1, 2, \dots, q \end{aligned} \]
对应的拉格朗日函数L为,
\[ L(\mathbf{x}, \lambda, \mu) = f(\mathbf{x}) + \sum_{j=1}^{p} \lambda_j h_j(\mathbf{x}) + \sum_{k=1}^{q} \mu_k g_k(\mathbf{x}) \]
常用的方法是KKT条件,即最优值必须满足:
\[ \begin{aligned} \frac{\partial F}{\partial x_i} = 0 \quad &(1)\\ \frac{\partial F}{\partial \lambda_j} = 0 \quad &(2)\\ \lambda_j \neq 0 \quad &(3)\\ \mu_k g_k(\mathbf{x}) = 0 \quad &(4)\\ g_k(\mathbf{x}) \leq 0 \quad &(5)\\ \mu_k \geq 0 \quad &(6) \end{aligned} \]
其中前三个式子是等式条件约束里的,后三个式子是不等式条件引入的。
KKT推导
\(\max_\mu L(x,\mu)\)代表调整\(\mu\)最大化目标函数\(L(x,\mu)\)。
首先,令(这里的几个变量都是多元变量,即向量,为了书写方便,没有引入
\mathbf)
\[ \ L(x, \lambda, \mu) = f(x) + \sum_{k=1}^{q} \mu_k g_k(x) \]
引入约束条件,
\[ \because \begin{cases} \mu_k \geq 0 \\ g_k(x) \leq 0 \end{cases} \\ \\ \therefore \mu_k g_k(x) \leq 0 \\ \therefore 根据非负得\ \max_\mu L(x,\mu)=f(x) \\ \therefore \min_ x f(x) = \min_x \max_ \mu L(x,\mu) \]
所以我们发现调整\(\mu\)最大化\(L\)就等于\(f(x)\),所以
\[ \min_ x f(x) = \min_x \max_ \mu L(x,\mu) \]
另一方面,
\[ \max_\mu \min_x L(x, \mu) = \max_\mu \left[ \min_x f(x) + \min_x \mu g(x) \right] = \max_\mu \min_x f(x) + \max_\mu \min_x \mu g(x) = \min_x f(x) + \max_\mu \min_x \mu g(x) \\ 又\because \begin{aligned} \mu_k \geq 0, \quad g_k(x) \leq 0 \quad &\Rightarrow \quad \min_x \mu g(x) = \begin{cases} 0, & \text{if } \mu = 0 \text{ or } g(x) = 0 \\ -\infty, & \text{if } \mu > 0 \text{ and } g(x) < 0 \end{cases} \end{aligned} \]
所以,引入约束条件\(\mu g(X)=0\),我们得到,
\[ \max_\mu \min_x \mu g(x) = 0 \\ \therefore \max_\mu \min_x L(x, \mu) = \min_x f(x) + \max_\mu \min_x \mu g(x) = \min_x f(x) \]
综上所述,
\[ \begin{aligned}\begin{rcases} L(x, \lambda, \mu) &= f(x) + \sum_{k=1}^{q} \mu_k g_k(x) \\ \mu_k &\geq 0 \\ g_k(x) &\leq 0 \\ \mu g(X)&=0 \end{rcases} \end{aligned} \Rightarrow \max_\mu \min_x L(x, \mu)= \min_x \max_ \mu L(x,\mu)=\min_ x f(x) \]
引入等式约束的条件,我们得到了,
\[ \begin{aligned}\begin{rcases} \frac{\partial F}{\partial x_i} = 0\\ \frac{\partial F}{\partial \lambda_j} = 0\\ \lambda_j \neq 0\\ \mu_k g_k(\mathbf{x}) = 0\\ g_k(\mathbf{x}) \leq 0\\ \mu_k \geq 0 \end{rcases} \end{aligned} \Rightarrow \max_\mu \min_x L(x, \mu)= \min_x \max_ \mu L(x,\mu)=\min_ x f(x) \]
所以我们完成了我们需要证明的:在一些列约束条件下,拉格朗日函数等同于优化的目标函数。
补充KTT下的隐藏条件:
\[ \frac{\partial L(x, \lambda, \mu)}{\partial x} \Bigg|_{x = x^*} = 0 \quad \text{表明} \quad f(x) \text{在极值点} x^* \text{处的梯度是含有} h_j(x^*) \text{和} g_k(x^*) \text{梯度的线性组合。} \]



