介绍
OneBit属于量化方法中的量化感知训练QAT。基于BitNet的OneBit将LLM的权重矩阵量化为1位,用一种新颖的 1 位参数表示方法以更好地量化 LLM,以及一种基于矩阵分解的有效参数初始化方法以提高量化框架的收敛速度。
方法
BitLinear
OneBit follow的工作是BitNet,BitNet提出BitLinear,BitLinear的forward函数为:
\[ \begin{align*} & \mathbf{W}_{\pm 1} = \operatorname{Sign}\left( \mathbf{W} - \operatorname{Mean}(\mathbf{W}) \right), \\ & \eta = \operatorname{Mean} \left( \operatorname{Abs} \left( \mathbf{W} - \operatorname{Mean}(\mathbf{W}) \right) \right), \\ & \mathbf{Y} = \eta \cdot \operatorname{LayerNorm}(\mathbf{X}) \mathbf{W}_{\pm 1}^{\top}, \end{align*} \]
其中,\(W\)表示量化后的权重矩阵,形状为 \(m \times n\),\(W_{±1}\)表示 1 位量化矩阵。\(X\)是线性层的输入,\(Y\) 是输出。函数 \(Sign()\)、\(Mean()\) 和 \(Abs()\) 分别返回符号矩阵、平均值和绝对值矩阵。
作者认为,缺失的浮点精度仍然破坏了模型性能,因此额外引入了两个始终保持fp16精度的向量:
\[ \begin{align*} & \mathbf{W}_{\pm 1} = \operatorname{Sign}(\mathbf{W}), \\ & \mathbf{Y} = \left[ (\mathbf{X} \odot \mathbf{g}) \mathbf{W}_{\pm 1}^{\top} \right] \odot \mathbf{h}, \\ & \mathbf{Z} = \operatorname{LayerNorm}(\mathbf{Y}), \end{align*} \]
其中的\(g\)和\(h\)是fp16精度的向量,\(Z\)是最终的输出。同时括号严格要求了计算顺序从而减小计算成本。其余的和BitNet保持一致。
训练的时候,不需要保存一个高精度的参数矩阵,只需要保存两个高精度的向量即可。
SVID
为了可以使用训练好的模型的ckpt来初始化量化模型的权重,这篇论文还引入了Sign-Value-Independent Decomposition (SVID),所以近似初始化方法为,
\[ \mathbf{W} \approx \mathbf{W}_{\text{sign}} \odot (\mathbf{a} \mathbf{b}^{\top}) \]
就是用训练好模型的权重矩阵\(W\),分解为量化模型的三部分\(\mathbf{W}_{\text{sign}} , \mathbf{a} , \mathbf{b}\)。
这里提出两个命题来说明合理性:
命题一:使用上面的近似,我们可以得到,
\[ \mathbf{X} \mathbf{W}^{\top} \approx \left[ (\mathbf{X} \odot \mathbf{b}^{\top}) \mathbf{W}_{\text{sign}}^{\top} \right] \odot \mathbf{a}^{\top} \]
根据这个命题,可以从近似初始化得到BitLinear的forward公式。
证明过程:
令\(s_{ij}\)为1Bit矩阵\(W_{sign}\)的一个元素,我们很容易得到:\(w_{i,j} \approx s_{i,j} \cdot a_i b_j\) 。
因此,我们有,
\[ \begin{align*} \left( \mathbf{X} \mathbf{W}^{\top} \right)_{ij} & = \sum_k x_{ik} w_{kj} \\ & = \sum_k x_{ik} w_{jk} \\ & \approx \sum_k x_{ik} s_{jk} a_j b_k \\ & = \sum_k x_{ik} b_k s_{jk} a_j \\ & = \sum_k \left( \mathbf{X} \odot \mathbf{b}^{\top} \right)_{ik} s_{kj}^{\top} a_j \\ & = \left[ \left( \mathbf{X} \odot \mathbf{b}^{\top} \right) \mathbf{W}_{\text{sign}}^{\top} \right]_{ij} a_j \\ & = \left\{ \left[ \left( \mathbf{X} \odot \mathbf{b}^{\top} \right) \mathbf{W}_{\text{sign}}^{\top} \right] \odot \mathbf{a}^{\top} \right\}_{ij} \end{align*} \]
命题二:给定矩阵 $W $和 \(|W|\),其中 \(W = W_{\text{sign}} \odot |W|\)。以如下方式对这些矩阵进行分解:\(W = \mathbf{a} \mathbf{b}^{\top} + \mathbf{E}_1\)和\(|W| = \tilde{\mathbf{a}} \tilde{\mathbf{b}}^{\top} + \mathbf{E}_2\),其中\(E_i\)表示误差矩阵。就 Frobenius 范数而言,SVD 分解比原始矩阵 $W $更接近:
\[ \left\| W - W_{\text{sign}} \odot \tilde{\mathbf{a}} \tilde{\mathbf{b}}^{\top} \right\|_F^2 \leq \left\| W - \mathbf{a} \mathbf{b}^{\top} \right\|_F^2. \]
根据这个命题,可以说明提出符号位可以更好地减小误差。
引理 1 令 \(\sigma_i(\mathbf{W})\) 表示矩阵 \(\mathbf{W}\) 的第 \(i\) 大奇异值。则以下不等式成立:
\[ \sigma_1(|\mathbf{W}|) \geq \sigma_1(\mathbf{W}). \]
引理证明 根据诱导范数的定义,有
\[ \sigma_1(\mathbf{W}) = \|\mathbf{W}\|_2 = \max_{\mathbf{x}, \|\mathbf{x}\|_2=1} \|\mathbf{W} \mathbf{x}\|_2, \]
\[ \sigma_1(|\mathbf{W}|) = \||\mathbf{W}|\|_2 = \max_{\mathbf{y}, \|\mathbf{y}\|_2=1} \||\mathbf{W}| \mathbf{y}\|_2. \]
注意对于任意 \(\mathbf{x}\),\(\|\mathbf{x}\|_2 = 1\),我们有
\[ \||\mathbf{W}| \mathbf{x}\|_2^2 = \sum_i \left( \sum_j |w_{ij}||x_j| \right)^2 \geq \sum_i \left( \sum_j w_{ij} x_j \right)^2 = \|\mathbf{W} \mathbf{x}\|_2^2. \]
因此
\[ \max_{\mathbf{y}, \|\mathbf{y}\|_2=1} \||\mathbf{W}| \mathbf{y}\|_2 \geq \max_{\mathbf{x}, \|\mathbf{x}\|_2=1} \|\mathbf{W} \mathbf{x}\|_2. \]
该引理得证。
命题证明 考虑通过 SVD 来证明。对于 SVD 分解,因为使用两个向量近似,等同于只保留最大的奇异值和对应的特征向量,rank-1 近似中的误差矩阵 \(\mathbf{E}\) 的范数等于所有奇异值平方和中除去最大奇异值后的总和。我们有
\[ \|\mathbf{E}_1\|_F^2 = \sum_{i=2}^n \sigma_i^2(\mathbf{W}), \]
\[ \|\mathbf{E}_2\|_F^2 = \sum_{i=2}^n \sigma_i^2(|\mathbf{W}|). \]
根据 \(\|\mathbf{W}\|_F^2 = \||\mathbf{W}|\|_F^2\),我们有
\[ \sum_{i=1}^n \sigma_i^2(\mathbf{W}) = \sum_{i=1}^n \sigma_i^2(|\mathbf{W}|). \]
根据引理 1,我们可以得出
\[ \|\mathbf{E}_1\|_F^2 \geq \|\mathbf{E}_2\|_F^2. \]
根据该命题中的方程,我们可以表示
\[ \mathbf{W}_{\text{sign}} \odot |\mathbf{W}| = \mathbf{W}_{\text{sign}} \odot (\tilde{\mathbf{a}} \tilde{\mathbf{b}}^{\top} + \mathbf{E}_2). \]
因此我们有
\[ \mathbf{W} - \mathbf{W}_{\text{sign}} \odot \tilde{\mathbf{a}} \tilde{\mathbf{b}}^{\top} = \mathbf{W}_{\text{sign}} \odot \mathbf{E}_2. \]
因此
\[ \|\mathbf{W}_{\text{sign}} \odot \mathbf{E}_2\|_F^2 = \sum_{i,j} s_{ij}^2 e_{ij}^2 = \sum_{i,j} e_{ij}^2 = \|\mathbf{E}_2\|_F^2 \leq \|\mathbf{E}_1\|_F^2, \]
其中 \(s_{ij} = \pm 1\) 是 \(\mathbf{W}_{\text{sign}}\) 的元素。由此,该命题中的不等式得证。
知识蒸馏
考虑在量化模型训练的时候加入知识蒸馏,大的教师模型代表量化前的模型,小的学生模型代表量化后的模型。损失由两部分组成,首先是交叉熵损失,
\[ \mathcal{L}_{\text{CE}} = -\frac{1}{n_s} \sum_{i=1}^{n_s} \sum_{c} P_c^{T}(o_i) \log P_c^{S}(o_i) \]
第二个是所以hidden states归一化后的差值的L2范数,
\[ \mathcal{L}_{\text{MSE}} = \sum_{i=1}^{n_s} \sum_{j=1}^{n_l} \left\| \frac{q_{i,j}^{T}}{\|q_{i,j}^{T}\|_2} - \frac{q_{i,j}^{S}}{\|q_{i,j}^{S}\|_2} \right\|_2^2 \]
总的损失为:
\[ \mathcal{L}_{\text{KD}} = \mathcal{L}_{\text{CE}} + \alpha \mathcal{L}_{\text{MSE}} \]
由于符号十分常用,因此这里省去对于其中的符号的解释说明。
训练的时候,使用是模拟量化进行训练,即原来的权重也会进行训练,部署的时候再压缩:
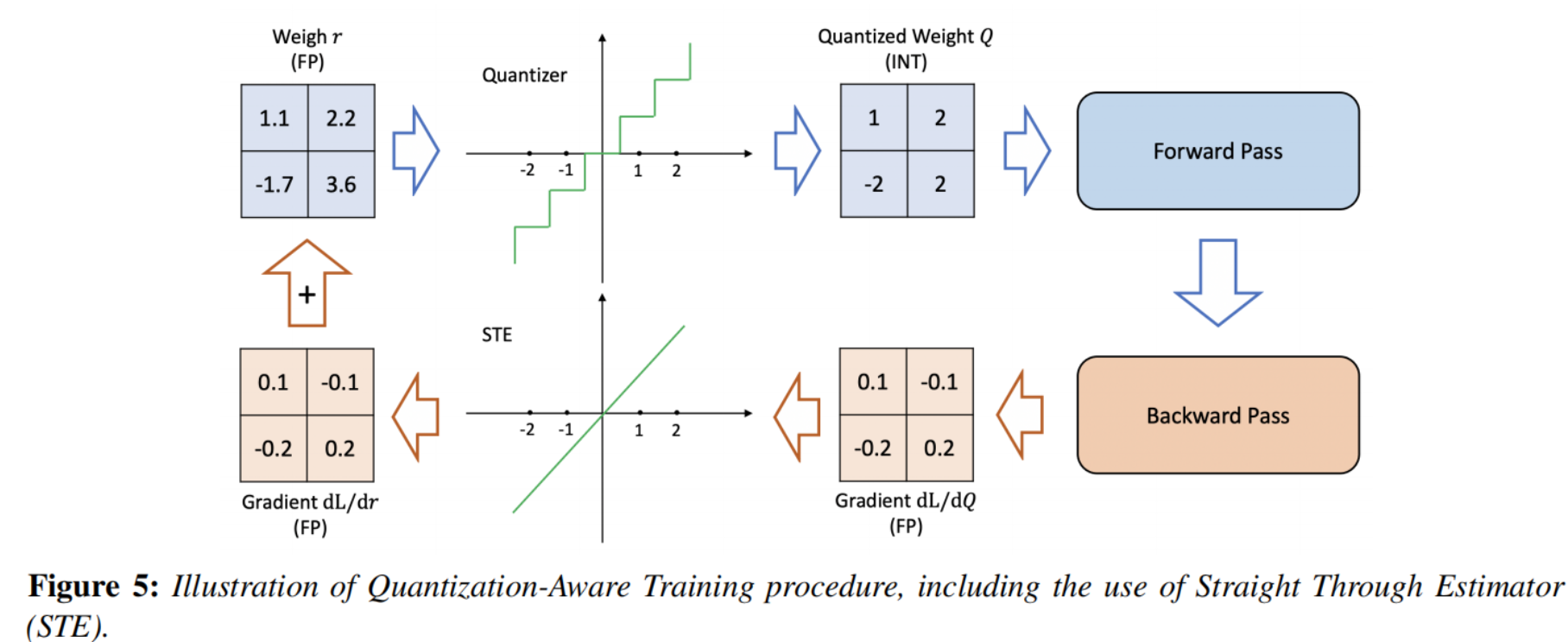
实验
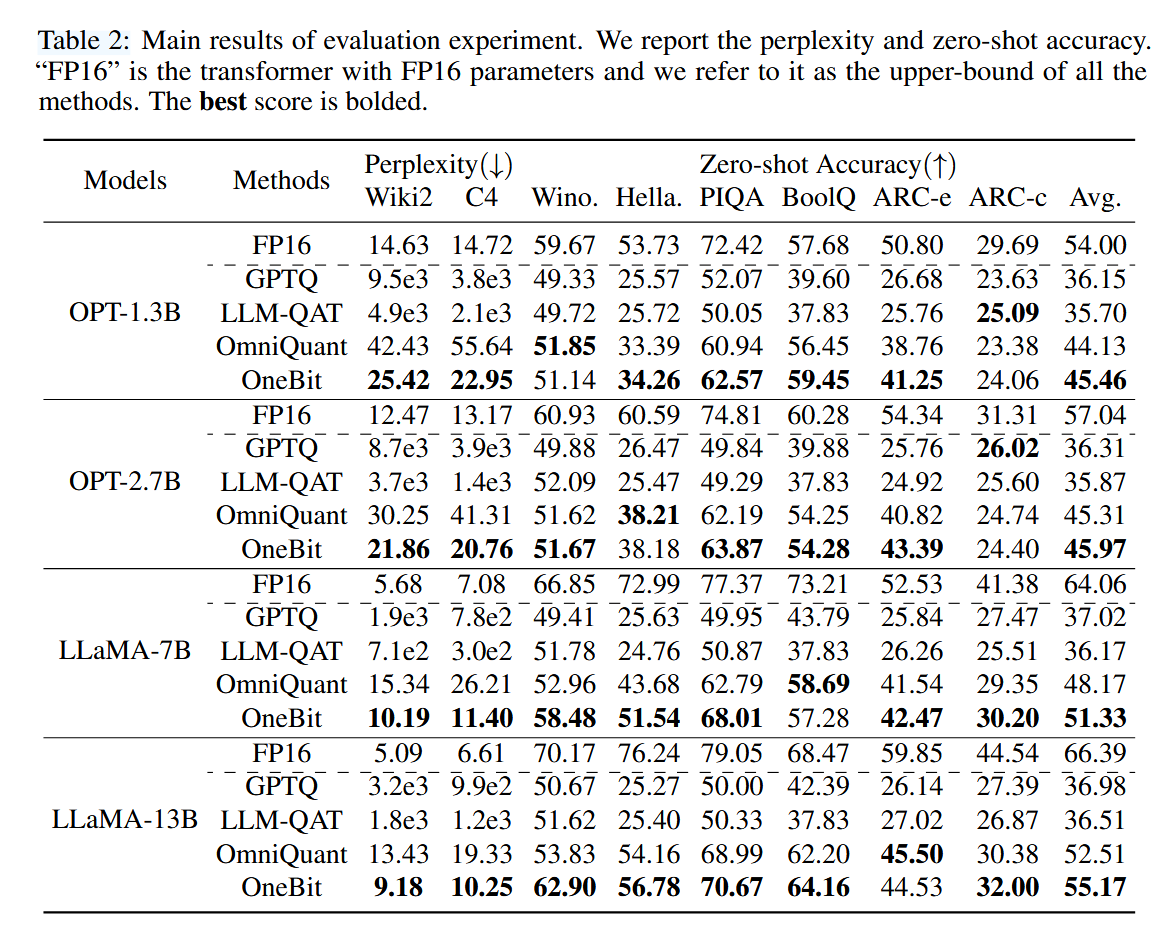
首先测试了该量化方法和一些PTQ方法和QAT方法的困惑度比较,其中的baseline为W2A16量化,本文方法为W1A16,可以看到取得了较大领先,
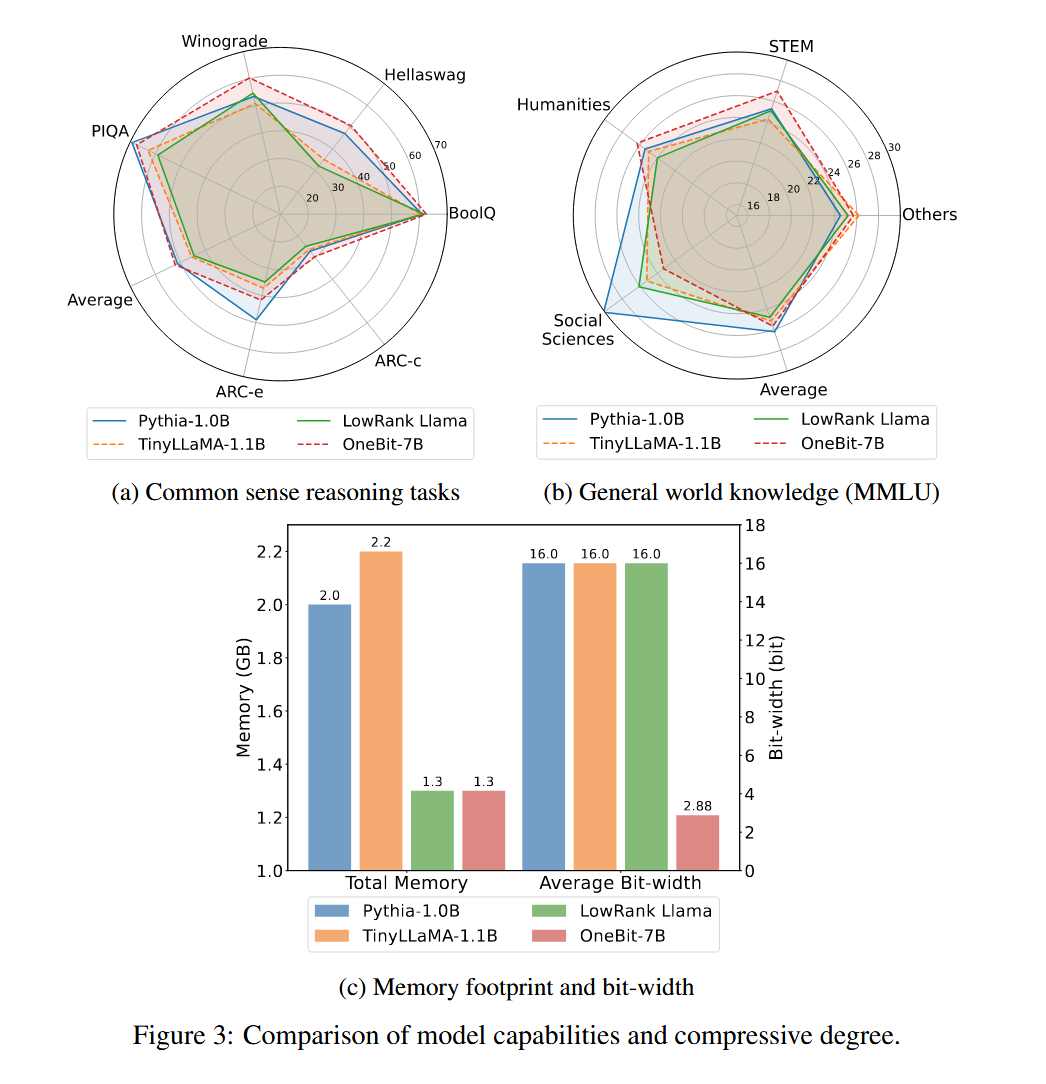
为了评估实际解决问题的能力,还测试了和一些小模型能力的差异和资源的需求,其中的OneBit是本文方法训练的模型,LowRank LLaMA是通过低秩分解压缩的Llama模型:
代码
论文源码:xuyuzhuang11/OneBit: The homepage of OneBit model quantization framework.
个人认为其中比较重要的部分:
- OneBit/transformers/src/transformers/models/bitnet.py at main · xuyuzhuang11/OneBit
- OneBit/scripts/build_start_ckpt.py at main · xuyuzhuang11/OneBit



