介绍
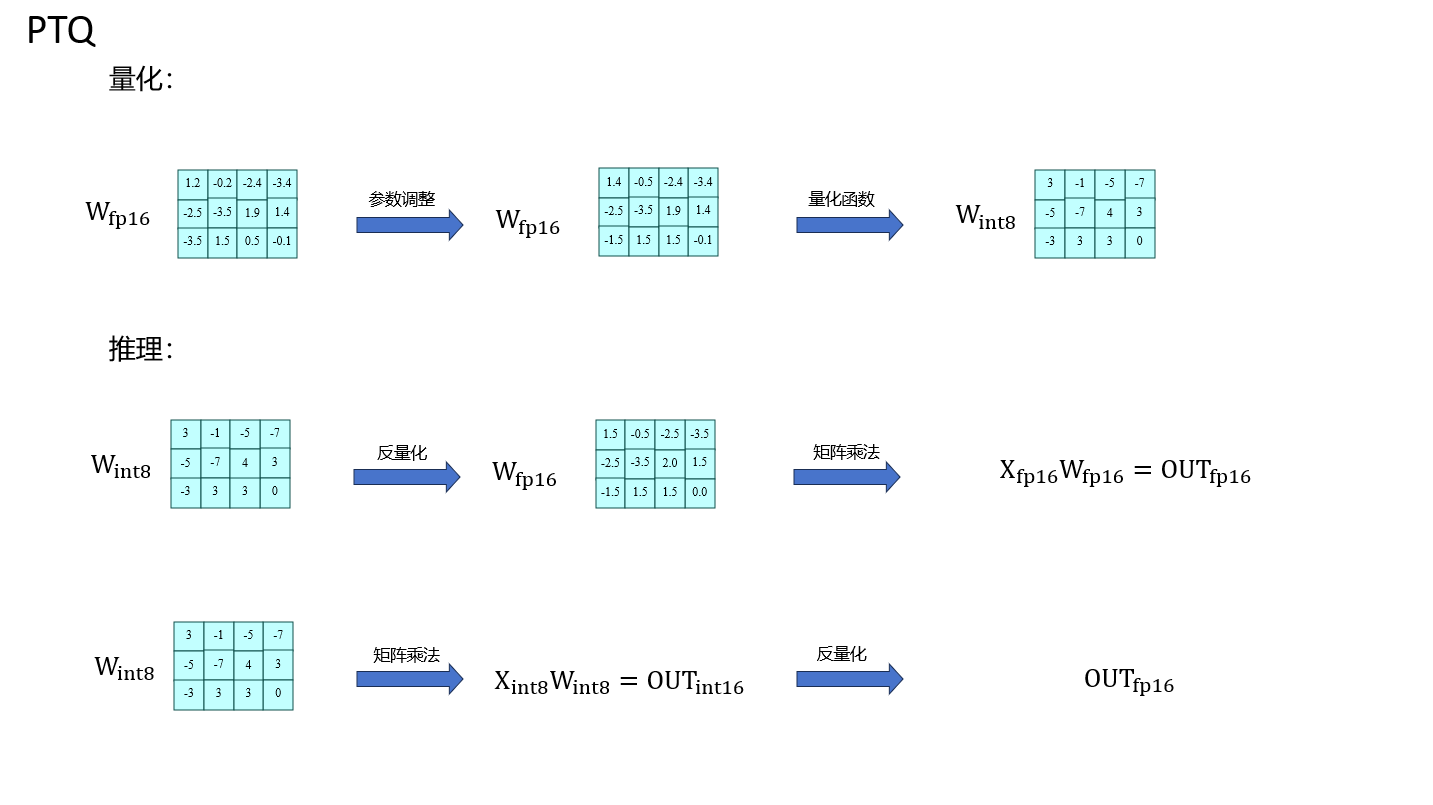
GPTQ算法的原理从数学公式出发,推导出权重的量化顺序和其余参数的调整值,然后根据这些值对block里的所有参数以列为单位进行量化,每次量化可以量化多个列,同时调整其余未量化的列的参数减小量化误差。
GPTQ算法是只针对权重的量化方式。在计算的时候,对应的内核会把需要计算的权重还原回原来的数据类型(比如int4->fp16)从而保证计算的稳定。
下图是PTQ大致流程图,GPTQ算法针对的主要是量化步骤中的参数调整部分:、
GPTQ量化算法最早来自1990年Yann LeCun的OBD算法,然后按照OBS,OBC(OBQ)的顺序进行演化,最终到GPTQ算法。当然,这里的演化算法不都是量化算法,由于量化和剪枝是很像的两个技术,量化调整参数为距离最近的整数,剪枝调整参数为0,所以量化算法和剪枝算法有很多共同点。
OBD:Optimal Brain Damage
OBD是一种剪枝方法,考虑目标函数为\(E\),模型参数为\(w_i\),对目标函数进行泰勒展开,有
\[ \Delta E = \sum_i g_i \Delta w_i + \frac{1}{2} \sum_i h_{ii} \Delta w_i^2 + \frac{1}{2} \sum_{i \neq j} h_{ij} \Delta w_i \Delta w_j + O(\Delta w^3) \]
其中\(g_i = \frac{\partial E}{\partial w_i}\)是一阶偏导,\(h_{ij} = \frac{\partial^2 E}{\partial w_i \partial w_j}\)是海森矩阵元素。
OBD假设:
- 目标函数为二阶,不考虑高阶项\(O(\Delta w^3)\)
- 模型训练充分收敛,一阶偏导为0,\(g_i=0,\forall i\)
- 每个参数对目标函数影响是独立的,海森矩阵中的交叉项为0,即\(h_{ij} = 0, \forall i, j, i \neq j\)
于是,上式可以优化为,
\[ \Delta E = \frac{1}{2} \sum_i h_{ii} \Delta w_i^2 \]
因此,OBD算法只需要根据每个参数对目标的影响从小到大进行排序,然后进行剪枝即可。
OBS:Optimal Brain Surgeon
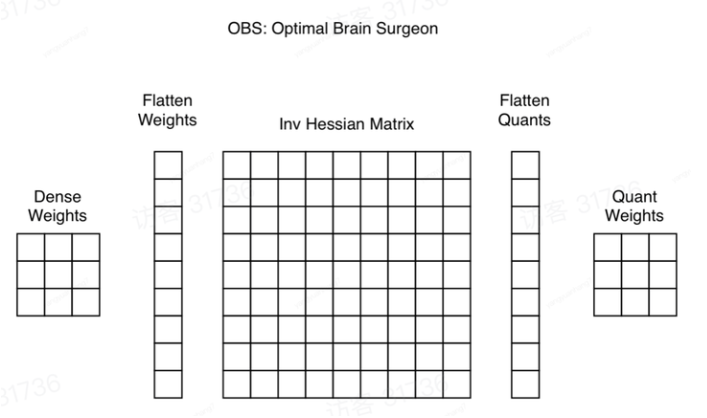
OBS算法认为参数之间的独立性不成立,因此交叉项需要考虑,因此上式变为,
\[ \Delta E = \frac{1}{2} \sum_i h_{ii} \Delta w_i^2 + \frac{1}{2} \sum_{i \neq j} h_{ij} \Delta w_i \Delta w_j \]
向量,矩阵形式为,
\[ \Delta E = \frac{1}{2} \Delta \mathbf{w}^\mathrm{T} \mathbf{H} \Delta \mathbf{w} \]
剪枝删除一个权重,那么\(\Delta \mathbf{w}\)的第 q 维固定为 \(-w_q\) ,但其他维度的值不固定,可以用于减少删除该权重带来的目标偏离。即约束条件为,
\[ \mathbf{e}_q^\mathrm{T} \cdot \Delta \mathbf{w} + w_q = 0 \]
其中,\(\mathbf{e}_q\)是one-hot 向量,第q个位置是1,其余位置为0。
所以剪枝转化为最优化问题,
\[ \min_{\Delta \mathbf{w}, q} \frac{1}{2} \Delta \mathbf{w}^\mathrm{T} \mathbf{H} \Delta \mathbf{w} \quad \text{s.t.} \quad \mathbf{e}_q^\mathrm{T} \cdot \Delta \mathbf{w} + w_q = 0 \]
构造拉格朗日函数,
\[ L = \frac{1}{2} \Delta \mathbf{w}^\mathrm{T} \mathbf{H} \Delta \mathbf{w} + \lambda (\mathbf{e}_q^\mathrm{T} \cdot \Delta \mathbf{w} + w_q) \]
求解,得
\[ \Delta \mathbf{w} = -\frac{w_q}{[\mathbf{H}^{-1}]_{qq}} \mathbf{H}^{-1} \cdot \mathbf{e}_q \quad \text{and} \quad L = \frac{1}{2} \frac{w_q^2}{[\mathbf{H}^{-1}]_{qq}} \]
因此,我们可以根据海森矩阵求得下一个剪枝的参数和其他参数调整的值。
每次更新参数都需要重新求解海森矩阵,原论文中提到了数学上的优化方法,但是较为复杂且在后续算法没有使用,此处不予列出。
OBC
由于需要求解全参数的海森矩阵甚至逆矩阵,复杂度极高,在参数规模上去后求解是不现实的。
因此假设:
- 在一个矩阵中只有同一行的参数是相关的
同时,为了更好的求解,对于一个维度为\((d_{row},d_{col})\)参数矩阵设置一个优化的目标函数,\(\mathbf{W}_{i,\cdot},\hat{\mathbf{W_{i,\cdot}}}\)分别是参数调整前后的权重向量
\[ E = \sum_{i=1}^{d_{\text{row}}} \| \mathbf{W}_{i,\cdot} \mathbf{X} - \hat{\mathbf{W}}_{i,\cdot} \mathbf{X} \|_2^2 \]
求每行的海森矩阵,
\[ \frac{\partial E}{\partial \hat{\mathbf{W}}_{i,\cdot}^2} = \mathbf{H}_i = 2 \mathbf{X} \mathbf{X}^\mathrm{T}, \quad \forall i = 1, 2, \dots, d_{\text{row}} \]
之后就可以求得矩阵每一行的剪枝顺序。
算法伪代码:

首先遍历每一行,然后重复k次,每次找到对目标函数影响最小的参数p,对p进行剪枝同时更新其他参数,删除海森矩阵的p行p列(不包括\(H_{pp}\)),再求逆。(这里罗列的好像是降低复杂度后的数学等效。)
OBC论文也罗列了一些别的性能上的优化,在后续算法没有使用,此处不予列出。
此处数学等效的方法是高斯消元,海森矩阵移除k行k列但包括\(H_{kk}\),因为左乘矩阵代表对行向量线性组合对,右乘矩阵代表对列向量线性组合,因此通过高斯消元即可实现对0的操作。证明可以从GPTQ的Cholesky证明中基本无条件的迁移。
OBQ
OBQ (和OBC是同一篇文章)指出,剪枝是一种特殊的量化(即剪枝的参数等价于量化到 0 点),因此只需要修改一下 OBC 的约束条件即可:
\[ \mathbf{e}_p^\mathrm{T} \cdot \Delta \mathbf{w} + w_p = \text{quant}(w_p) \]
相应的,权重的调整更新为,
\[ \Delta \mathbf{w} = -\frac{w_p - \text{quant}(w_p)}{[\mathbf{H}^{-1}]_{pp}} \mathbf{H}^{-1} \cdot \mathbf{e}_p \quad \text{and} \quad L = \frac{1}{2} \frac{(w_p - \text{quant}(w_p))^2}{[\mathbf{H}^{-1}]_{pp}} \]
OBQ的算法伪代码,同OBC的很相似:

GPTQ
OBQ的算法复杂度还是太高了,GPTQ继续进行优化。
GPTQ是逐层量化的,同时做出以下假设:
- 参数调整前量化网络(量化函数)是确定的,比如量化的缩放因子和零点等
- 权重参数可以在量化网格内进行调整
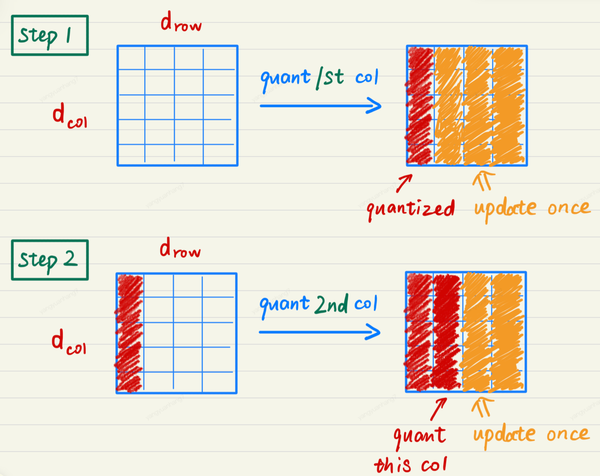
按索引顺序量化
将每一行的量化权重选择方式从贪心策略改成按索引顺序选择。
修改索引顺序的好处有两个,首先多个行的量化顺序是一样的,因此可以多行并行处理;第二个是\(\mathbf{H} = 2 \mathbf{X}
\mathbf{X}^\mathrm{T}\)说明,海森矩阵只与输入相关,因此不同行可以共用一个海森矩阵。
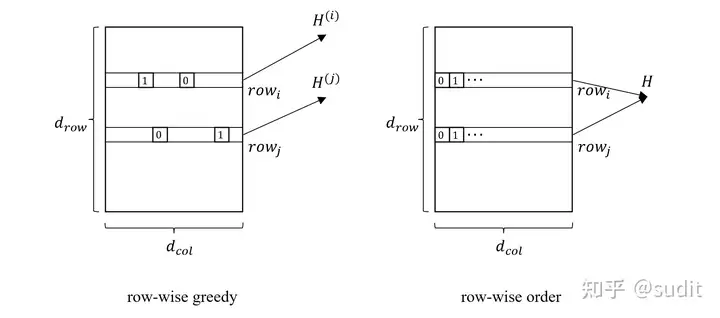
行里第p个权重调整公式可以为改为,
\[ \Delta \mathbf{w} = -\frac{w_p - \text{quant}(w_p)}{[\mathbf{H}_{p:,p:}^{-1}]_{0,0}} \left( [\mathbf{H}_{p:,p:}^{-1}]_{:,0} \right)^\top \]
加入多行并行后变为,
\[ \Delta W_{:,p:} = -\frac{W_{:,p:} - \text{quant}(W_{:,p:})}{[\mathbf{H}_{p:,p:}^{-1}]_{0,0}} \left( [\mathbf{H}_{p:,p:}^{-1}]_{:,0} \right)^\top =-\frac{\left( [\mathbf{H}_{p:,p:}^{-1}]_{:,0} \right)^\top}{[\mathbf{H}_{p:,p:}^{-1}]_{0,0}} ( W_{:,p:} - \text{quant}(W_{:,p:})) \]
逆矩阵的更新公式变为,
\[ [H_{p:,p:}]^{-1} = \left( [H_{p-1:,p-1:}]^{-1} - \frac{1}{[H_{p-1:,p-1:}]^{-1}_{0,0}} [H_{p-1:,p-1:}]^{-1}_{:,0} [H_{p-1:,p-1:}]^{-1}_{0,:}\right)_{1:,1:} \]
Cholesky 分解
关于Cholesky分解的数学介绍可以看:三十分钟理解:矩阵Cholesky分解,及其在求解线性方程组、矩阵逆的应用_cholesky分解法求解线性方程组-CSDN博客
实验过程中发现:在大规模参数矩阵上重复使用海森矩阵逆矩阵的更新公式会产生非正定的海森矩阵逆矩阵,原因可能是数值误差的积累。
作者对初始的\(H^{-1}\)进行Cholesky 分解,得到一个上三角矩阵\(T\),它的每一行刚好就等于使用更新公式得到的逆矩阵序列的第一行乘以一个常数,即,
\[ C_p T_{p,p:} = \left[ H_{p:,p:} \right]^{-1}_{0,:} \]
图示,
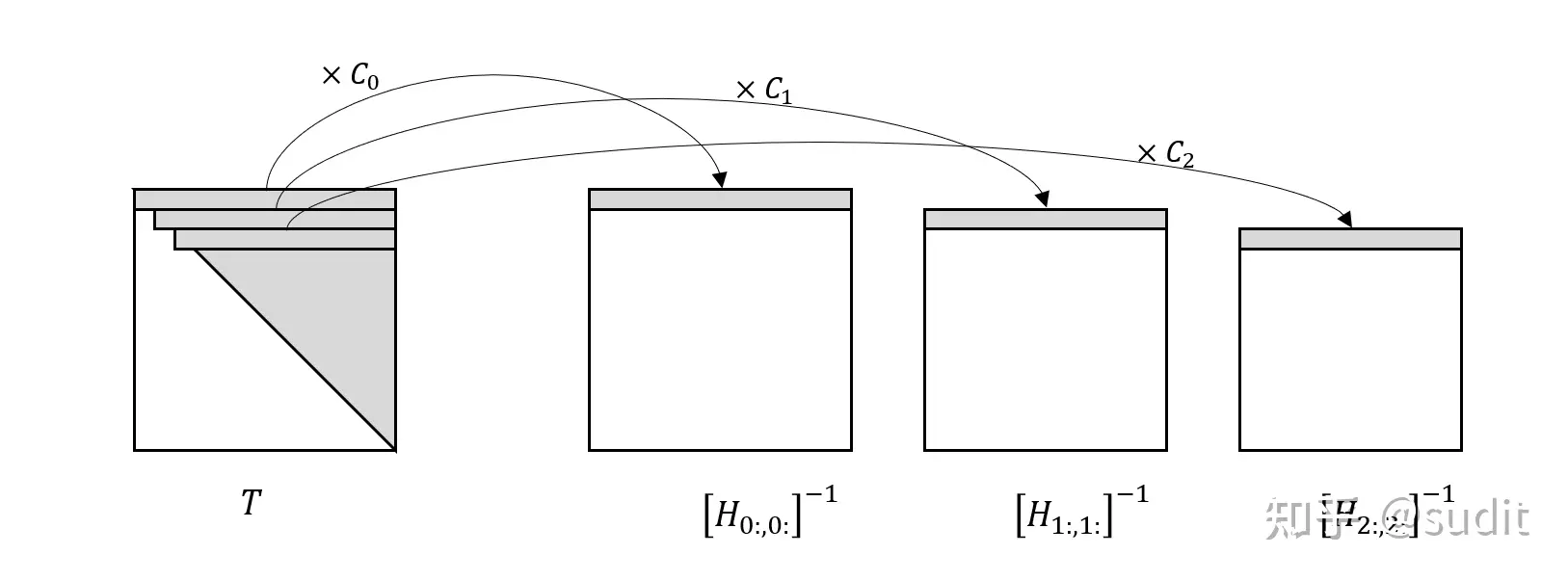
所以,权重的调整更新为,
\[ \Delta W_{:,p:} = - \frac{W_{:,p} - \text{quant}(W_{:,p})}{C_p T_{pp}} C_p T_{p,p:} = - \frac{W_{:,p} - \text{quant}(W_{:,p})}{T_{pp}} T_{p,p:} \]
发现很多资料都没有系统的罗列大致的推导过程,甚至论文基本也是一笔带过,因此考虑在此给出一些浅薄的证明(笔者不是数学系的。
首先介绍一下教程中的Cholesky分解:给定一个\(n\times n\)的实数对称正定矩阵\(A\),存在一个对角元全为正数的下三角矩阵,是的\(A=LL^\top\)成立。
\[ \begin{align*} \mathbf{A} &= \begin{bmatrix} a_{11} & \mathbf{A}_{21}^T \\ \mathbf{A}_{21} & \mathbf{A}_{22} \end{bmatrix}, \quad \mathbf{L} = \begin{bmatrix} l_{11} & 0 \\ L_{21} & L_{22} \end{bmatrix}, \quad \mathbf{L}^T = \begin{bmatrix} l_{11} & L_{21}^T \\ 0 & L_{22}^T \end{bmatrix} \end{align*} \]
其中 $a_{11} $ 和 $ l_{11} $是一个标量, \(\mathbf{A}_{21}\) 和 \(L_{21}\) 是一个列向量,${22} $是一个 ( n-1 ) 阶的方阵,而 $ L{22} $ 是一个 ( n-1 ) 阶的下三角矩阵。我们有,
\[ \begin{align*} \begin{bmatrix} a_{11} & \mathbf{A}_{21}^T \\ \mathbf{A}_{21} & \mathbf{A}_{22} \end{bmatrix} &= \begin{bmatrix} l_{11} & 0 \\ L_{21} & L_{22} \end{bmatrix} \begin{bmatrix} l_{11} & L_{21}^T \\ 0 & L_{22}^T \end{bmatrix} &= \begin{bmatrix} l_{11}^2 & l_{11} L_{21}^T \\ l_{11}L_{21} & L_{21} L_{21}^T + L_{22} L_{22}^T \end{bmatrix} \end{align*} \]
我们易得,
\[ \begin{align*} l_{11} &= \sqrt{a_{11}} \\[10pt] L_{21} &= \frac{1}{l_{11}} \mathbf{A}_{21} \\[10pt] L_{22} L_{22}^T &= \mathbf{A}_{22} - L_{21} L_{21}^T \end{align*} \]
其中\(l_{11}\)和\(L_{21}\)我们直接得到,对于\(L_{22}\),我们发现又是一个Cholesky分解的过程,递归求解即可。
我们根据公式可以发现,
\[ (\mathbf{L}^\top)_{1,:} =\begin{bmatrix} l_{11} & L^{\top}_{21} \end{bmatrix} = \frac{1}{\sqrt{a}} \begin{bmatrix} a_{11} & \mathbf{A}^{\top}_{21} \end{bmatrix} = \frac{1}{\sqrt{a}}\mathbf{A}_{1,:} \]
所以我们证明了两个矩阵第一列的比例关系,根据分解的递推性和矩阵的对称性,我们就完整证明了这个结论。
海森逆矩阵更新公式证明
首先我们需要证明在海森矩阵删除p行p列参数(不包括\(H_{pp}\))的时候,在海森矩阵上会发生类似的操作。
首先,我们需要知道\((H^{-1})^\top=(H^T)^{-1}=H^{-1}\),即海森矩阵的逆矩阵是对称矩阵。
\[ \begin{align*} \mathbf{H}= \begin{bmatrix} a & \mathbf{z}^\top \\ \mathbf{z} & \mathbf{A} \end{bmatrix}, \quad 构造矩阵\mathbf{B}=\begin{bmatrix} \frac{1}{a} & \mathbf{z}^\top \\ \mathbf{z} & \mathbf{A}^{-1} \end{bmatrix} \end{align*} \]
其中,\(\mathbf{H}\)和\(\mathbf{B}\)是n维的对称正定方阵,a\(是标量,\)\(z\)为n-1维的零向量,那么
\[ \mathbf{H} \times \mathbf{B}= \begin{bmatrix} a & \mathbf{z}^\top \\ \mathbf{z} & \mathbf{A} \end{bmatrix} \times \begin{bmatrix} \frac{1}{a} & \mathbf{z}^\top \\ \mathbf{z} & \mathbf{A}^{-1} \end{bmatrix} =\begin{bmatrix} 1 & a\mathbf{z}^\top+\mathbf{z}^\top\mathbf{A}^{-1} \\ \frac{1}{a}\mathbf{z}+\mathbf{A}\mathbf{z} & \mathbf{z}\mathbf{z}^\top+\mathbf{A}\mathbf{A}^{-1} \end{bmatrix} =\begin{bmatrix} 1 & \mathbf{z}^\top \\ \mathbf{z} & I_{n-1\times n-1} \end{bmatrix} =I_{n\times n} \]
说明,说明\(\mathbf{B}\)就是\(\mathbf{H}\)的逆矩阵,因此,得证。我们就可以直接对海森矩阵的逆矩阵进行删除参数即可。
接下来,我们需要证明删除行参数和列参数的公式。为了方便,假设我们有个n维的对称正定方阵\(\mathbf{A}\),令
\[ \mathbf{B}=\mathbf{A}-\frac{1}{\mathbf{A}_{11}}\mathbf{A}_{:,1}\mathbf{A}_{1,:} \]
那么,
\[ \mathbf{B}_{i,1}=\mathbf{A}_{i,1}-\frac{1}{\mathbf{A}_{11}}\mathbf{A}_{i1}\mathbf{A}_{11}=0,i \neq 1 \]
所以\(\mathbf{B}\)的第一列除了第一个元素全部为0,根据对称性,第一行也全部为0,即实现了对第一行第一列元素的删除。
尽管这里推导的时候是针对第一行或者第一列的,但是很容易外推到任意位置。
到此,我们证明了海森逆矩阵更新公式的正确性,分为两步:首先证明删除参数后海森逆矩阵的格式,然后根据格式证明了更新公式的正确性。
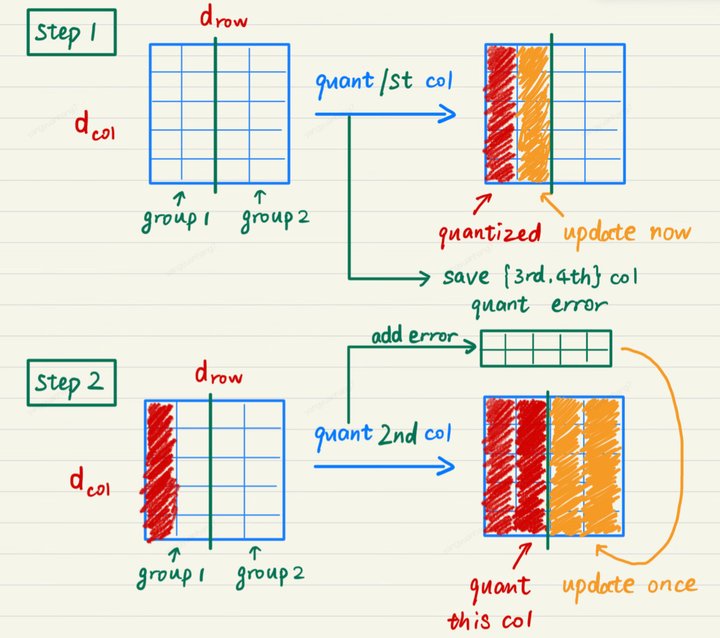
Lazy Batch-Updates
在量化某个参数矩阵的情况下,每次量化一个参数,其他所有未量化的参数都要按公式全都要更新一遍。如果每行的量化并行计算,那么每次更新过程就需要 read + write 一次参数矩阵。如果参数矩阵的维度为\(k \times k\),那么量化这个参数矩阵就需要读写 k 次参数,总共的 IO 量为\(k^3\)个元素。当 k 比较大时(>= 4096),需要读写的元素就非常多了,运行时间大都被 IO 占据。
\[ \Delta W_{:,p:} = -\frac{W_{:,p:} - \text{quant}(W_{:,p:})}{[\mathbf{H}_{p:,p:}^{-1}]_{0,0}} \left( [\mathbf{H}_{p:,p:}^{-1}]_{:,0} \right)^\top =-\frac{\left( [\mathbf{H}_{p:,p:}^{-1}]_{:,0} \right)^\top}{[\mathbf{H}_{p:,p:}^{-1}]_{0,0}} ( W_{:,p:} - \text{quant}(W_{:,p:})) \]
将参数矩阵按每若干列划分为一个个 group,量化某一列时,group 内的参数立即更新,而 group 后面的列只记录更新量,延迟更新。当一个 group 的参数全部量化完成,再统一对后面的所有参数做一次更新。这就是 Lazy Batch-Updates。根据更新公式我们可以发现,这个更新可以是可以合并同类项的,把一个group的第一项提出来求和,可以一次读写后面的所有group。
对应的算法伪代码为

实验
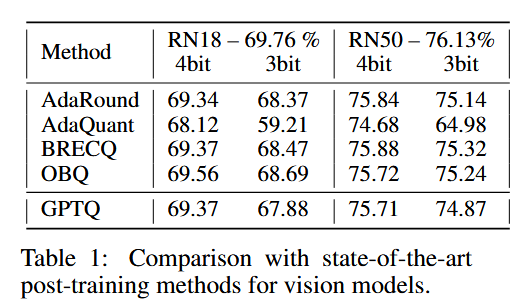
1.小模型测试
首先在ResNet上面进行了测试。选择AdaQuant、基于贪心策略的 OBQ在精度上保持持平。相比量化前的模型来说,性能也没有下降太多。
然后在小型语言模型上(这是OBQ能使用的最大的模型之一)进行了测试。在4bit得分比之前的方法稍微差一点,在3bit要低的多一点。
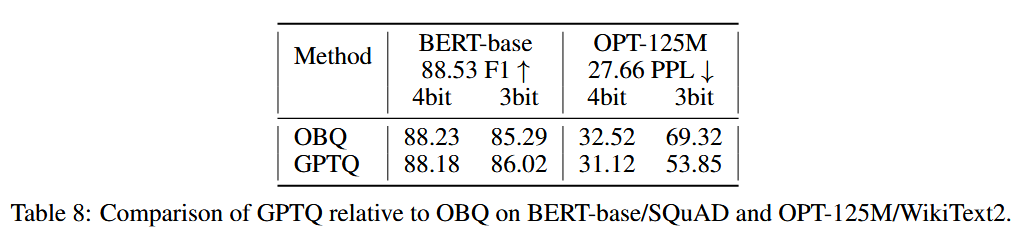
但是量化需要时间从1h降到1min。
2.测试了量化时间
提供了一个参考的标准:
"For reference, the straight-through based method ZeroQuant-LKD (Yao et al., 2022) reports a 3 hour runtime (on the same hardware) for a 1.3B model, which would linearly extrapolate to several hundred hours (a few weeks) for 175B models."
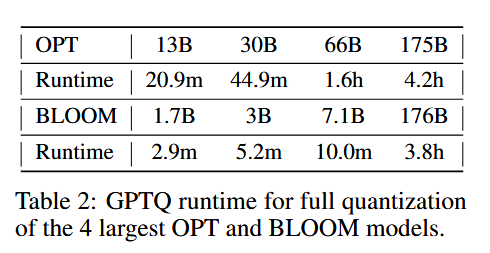
3.测试了量化模型在文本生成任务的表现
和不进行优化的直接量化(RTN)进行了对比。
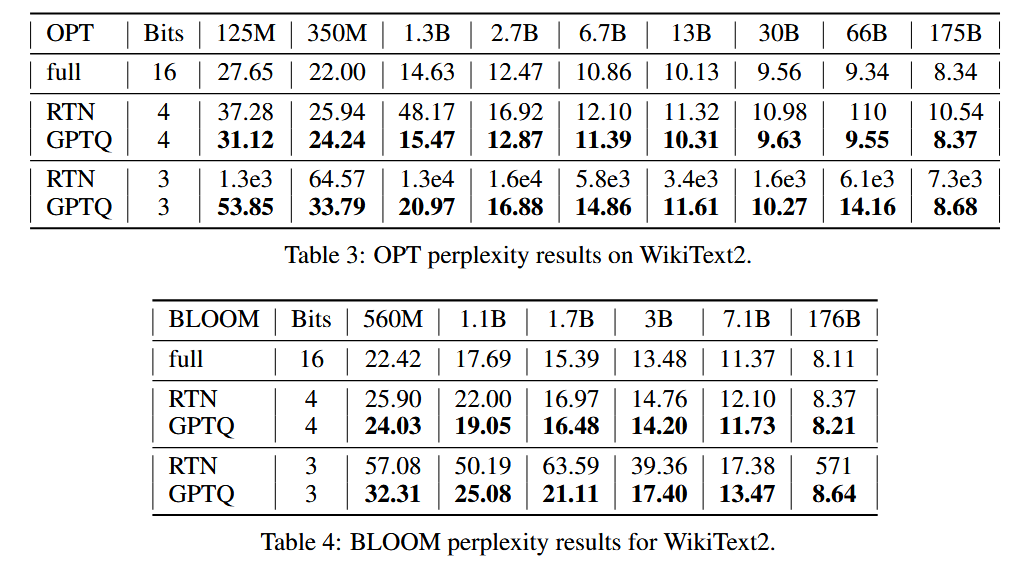
4.测试了OPT-175B文本生成的效率
开发了相关kernel(推理时权重会反量化),量化只针对权重,激活不量化。

5.零样本任务评测
测试了和基线相比,在零样本任务上的准确率。
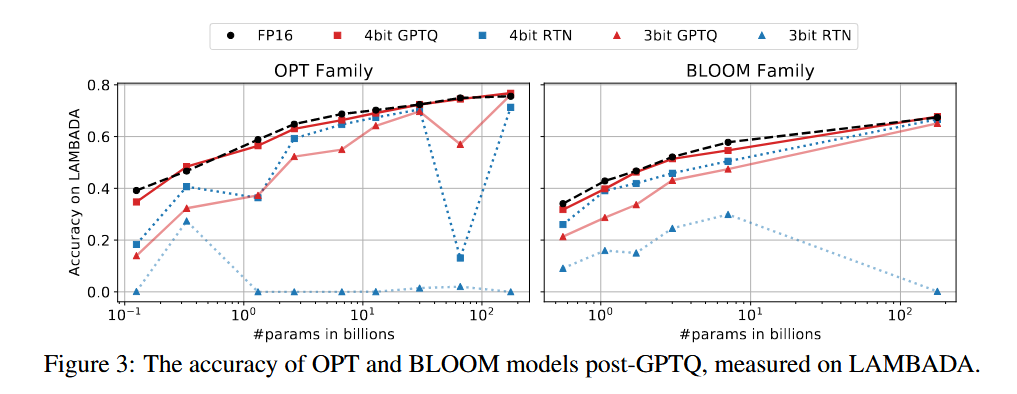
该方法很容易和别的量化网络相结合。量化网络指的是量化的操作,是权重调整后的具体量化步骤,需要确定比如缩放因子,零点,量化的粒度等。
代码解析
参考资料
- QLoRA、GPTQ:模型量化概述 - 知乎
- LLM 推理加速技术 —— GPTQ 量化技术演进 - 知乎
- [2210.17323] GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers
- AutoGPTQ/AutoGPTQ: An easy-to-use LLMs quantization package with user-friendly apis, based on GPTQ algorithm.
- IST-DASLab/gptq: Code for the ICLR 2023 paper "GPTQ: Accurate Post-training Quantization of Generative Pretrained Transformers".
- Optimal Brain Damage
- 三十分钟理解:矩阵Cholesky分解,及其在求解线性方程组、矩阵逆的应用_cholesky分解法求解线性方程组-CSDN博客



