介绍
本篇博客介绍论文[2306.00978] AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration提出的一种针对权重的训练后量化方法。该方法基于一个发现:模型的权重不是同等重要的,只保护 1%的突出权重可以大大减少量化误差。但是混合精度会导致算法对硬件不友好,具体保护的方法是对模型的权重进行扩大,输入也进行对应的缩小。具体的比例根据激活通过网格搜索获得。由于没有进行反向传播,因此量化模型在与校准数据集不同分布的数据上也能表现良好。并最终实现了推理加速效果。
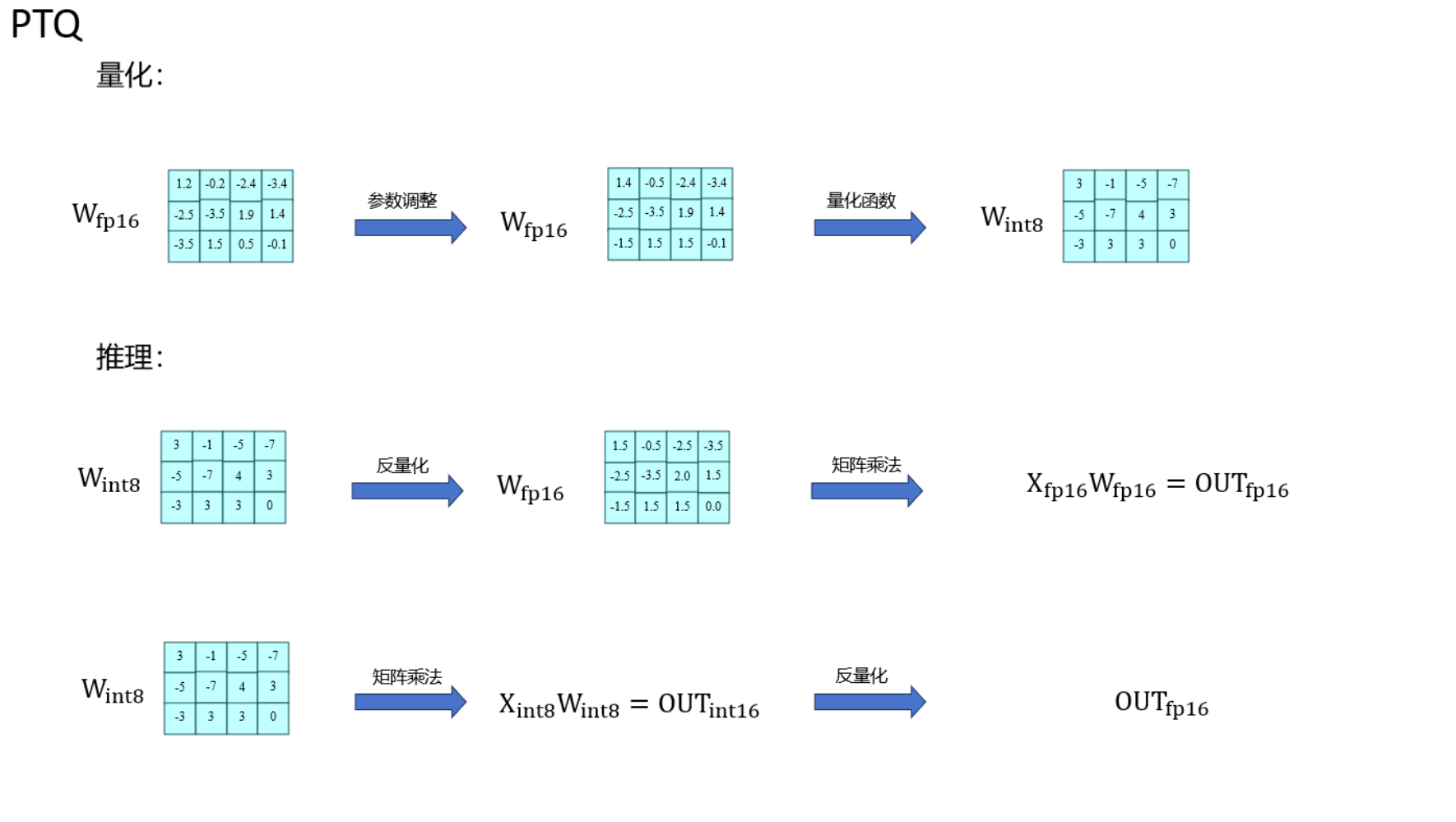
下图是PTQ大致流程图,和GPTQ算法一样,AWQ算法针对的主要是量化步骤中的参数调整部分:
发现
首先介绍作者根据经验提出的假设:模型的权重不是同等重要的,只保护 1%的突出权重可以大大减少量化误差。下图是示例:

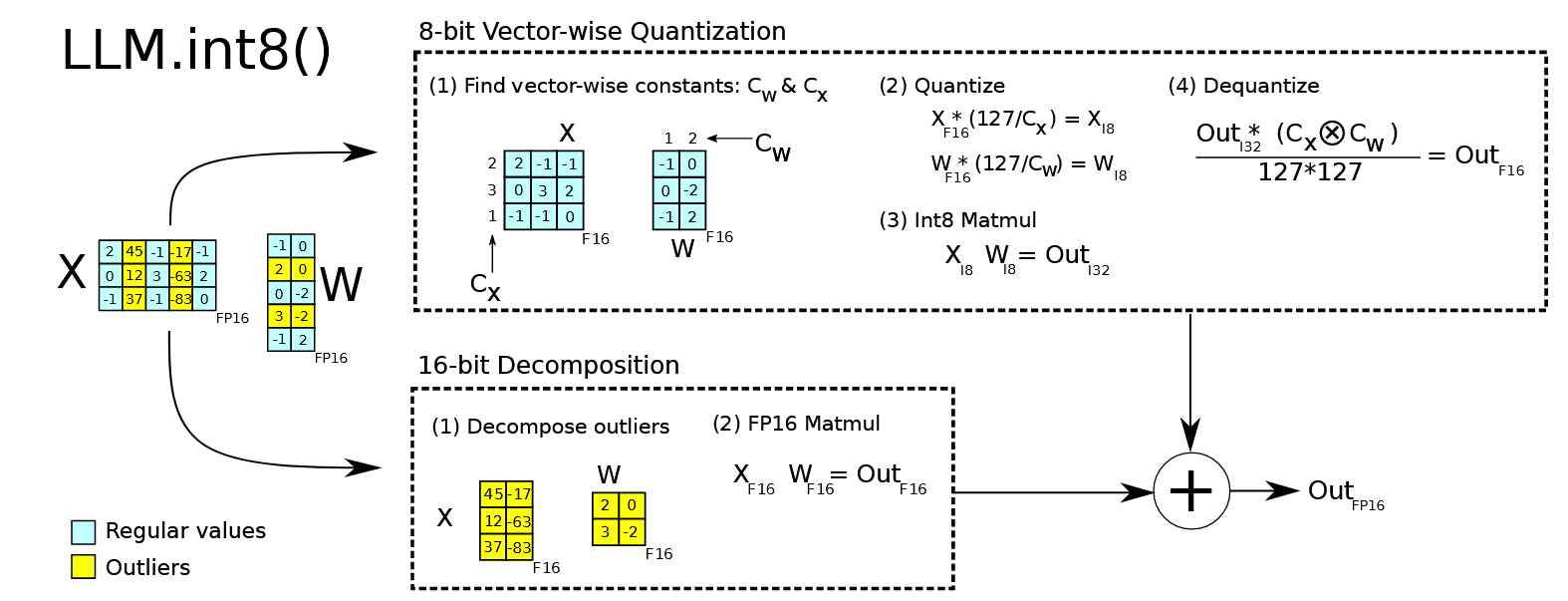
从图里可以看出,在某一层layer的输入中,不同token的异常维度应该是集中在某几个维度中的。在LLM.int8中也有类似的结论,并且因此设计了llm.int8算法:
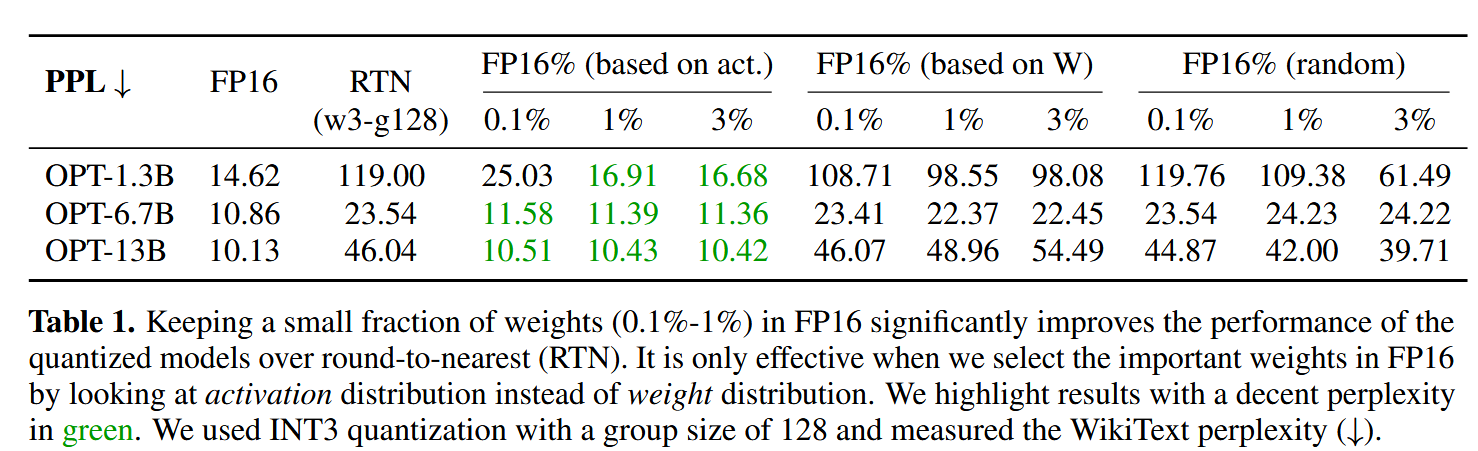
为了验证这个假设,作者进行了实验,尝试对少部分显著的权重保持原来精度,别的权重量化为int3,然后进行了多组测试。RTN是直接量化,不做调整,作为对比实验。作者分别尝试了使用权重的大小,激活的大小以及随机选择来确定哪些权重的显著的,结果发现根据激活选择的效果最好。
方法
根据发现,只需要根据激活选择少部分权重保持为高精度即可实现优秀的量化算法,但是混合精度是硬件不友好的操作。因此,作者选择别的方法来保护这些权重:通过激活感知缩放来保护显着权重。
考虑权重 \(\mathbf{w}\),线性层操作可以记为\(y = \mathbf{w} \mathbf{x}\), 对应的量化操作(包含反量化)为\(y = Q(\mathbf{w}) \mathbf{x}\),\(N\)是量化的比特数,\(\Delta\)是缩放因子,量化函数为:
\[ Q(\mathbf{w}) = \Delta \cdot \text{Round}\left(\frac{\mathbf{w}}{\Delta}\right), \quad \Delta = \frac{\max(|\mathbf{w}|)}{2^{N-1}} \]
考虑针对权重中的一个向量 $w $ 乘以 $s > 1 $ ,然后按同等比例缩小 $x $, 我们有 $Q(w s)(x / s) $, 具体为:
\[ Q(w \cdot s) \cdot \frac{x}{s} = \Delta' \cdot \text{Round}\left(\frac{w s}{\Delta}\right) \cdot x \cdot \frac{1}{s} \]
\(\Delta'\)是新的缩放因子。
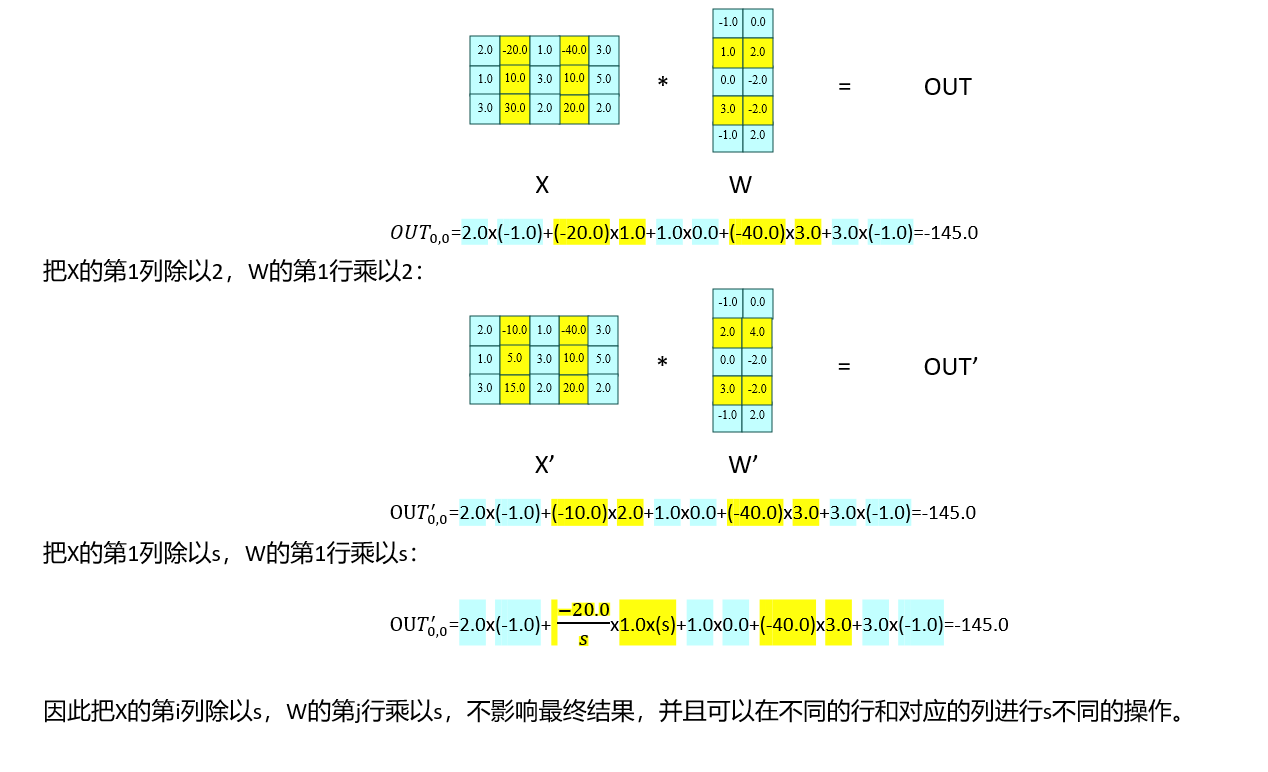
这里解释一下为什么放缩针对是一行(这里假设乘号左边是X,右边是W):
然后量化的时候,以列或者行作为量化函数的基本单位:
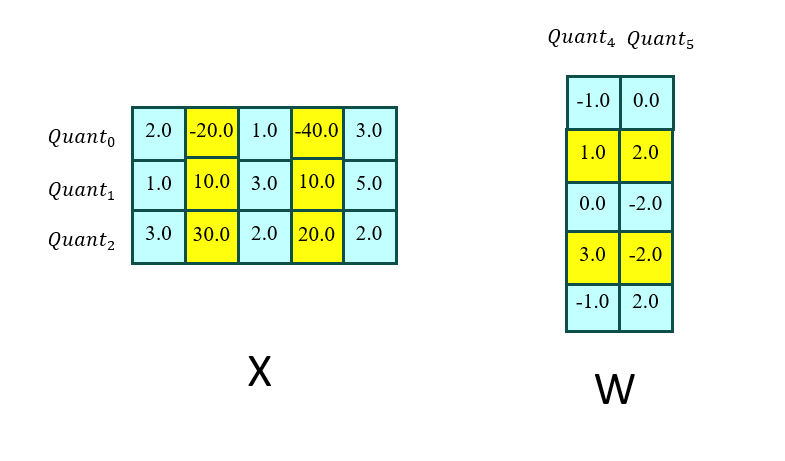
作者根据经验判断:
- 量化为整数(Round函数)的时候,误差在0~0.5之间均匀分布,因此,平均误差为0.25。因此在对权重放大后,相对误差会减小,比如之前值是1,相对误差为0.25,1放大2倍后,相对误差只有0.125。
- 对部分\(w\)进行放缩对量化时分组里的极值改变较少,因此\(\Delta' \approx \Delta\)
- 第二点的误差可以表示为\(\text{Err}' = \Delta' \cdot \text{RoundErr} \cdot \frac{1}{s}\),与原始误差的比例为\(\frac{\Delta'}{\Delta} \cdot \frac{1}{s}\)。如果\(\Delta' \approx \Delta,s>1\),那么就会降低误差
然后作者选择了一部分参数进行了验证:
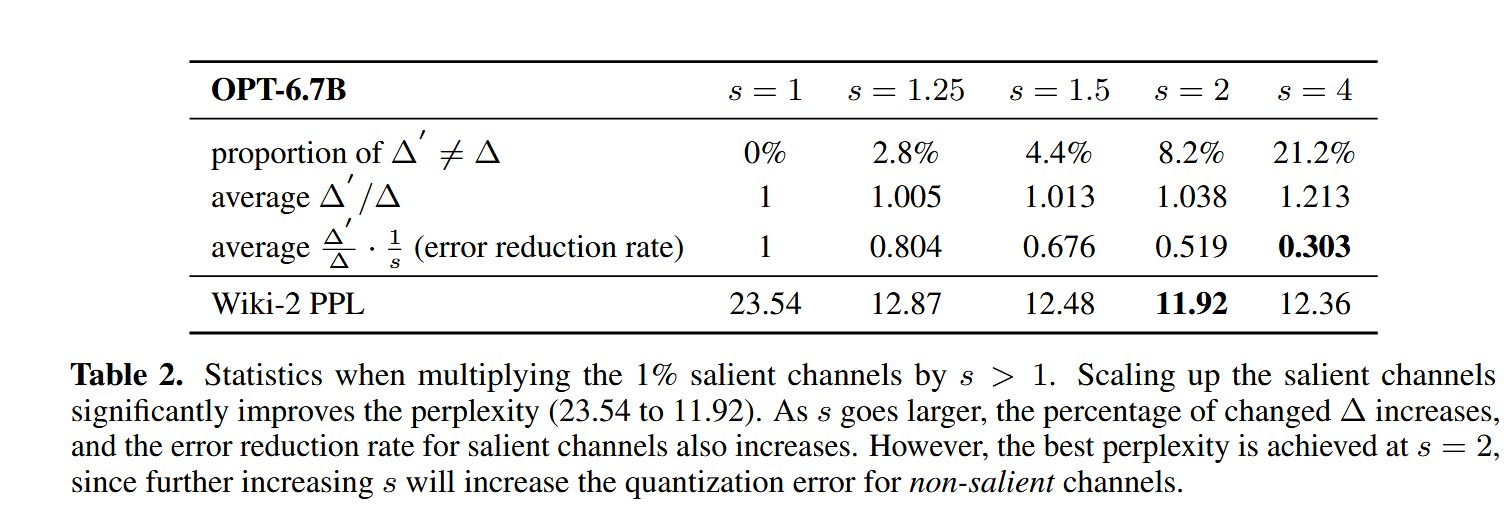
根据结果发现,在s=2的时候PPL达到了最小。在s不超过2的时候,基本符合根据经验得到的结论。
对于AWQ算法中的\(s\),作者认为这是一个最优化问题:
\[ \mathbf{s}^* = \arg \min_{\mathbf{s}} \, \mathcal{L}(\mathbf{s}), \quad \mathcal{L}(\mathbf{s}) = \left\| Q(\mathbf{W} \cdot \mathbf{s}) \left(\mathbf{s}^{-1} \cdot \mathbf{X}\right) - \mathbf{W} \mathbf{X} \right\| \]
由于量化函数不可微分,别的近似方法存在收敛不稳定的情况,作者最终根据激活使用网格搜索获得:
\[ \mathbf{s} = \mathbf{s}_{\mathbf{X}}^{\alpha}, \quad \alpha^* = \arg \min_{\alpha} \mathcal{L}(\mathbf{s}_{\mathbf{X}}^{\alpha}) \]
\(\mathbf{s} _{\mathbf{X}}\)和输入\(\mathbf{X}\)有关,\(\alpha\)搜索的范围在[0,1]之间。
作者通过实验验证了搜索的有效性:
此外,作者还进行了以下优化:
- 对扩大化的权重进行裁剪
- 把对输入的缩小和前一个算子融合(比如,以前一个算子是矩阵乘法作为例子:前一个矩阵权重权重缩小\(s\),对前一个算子来说,扩大比例和缩小的比例大小不一样,并且可能方向也不一样,比如一个是列方向,另一个是行方向,因此不会完全抵消
实验
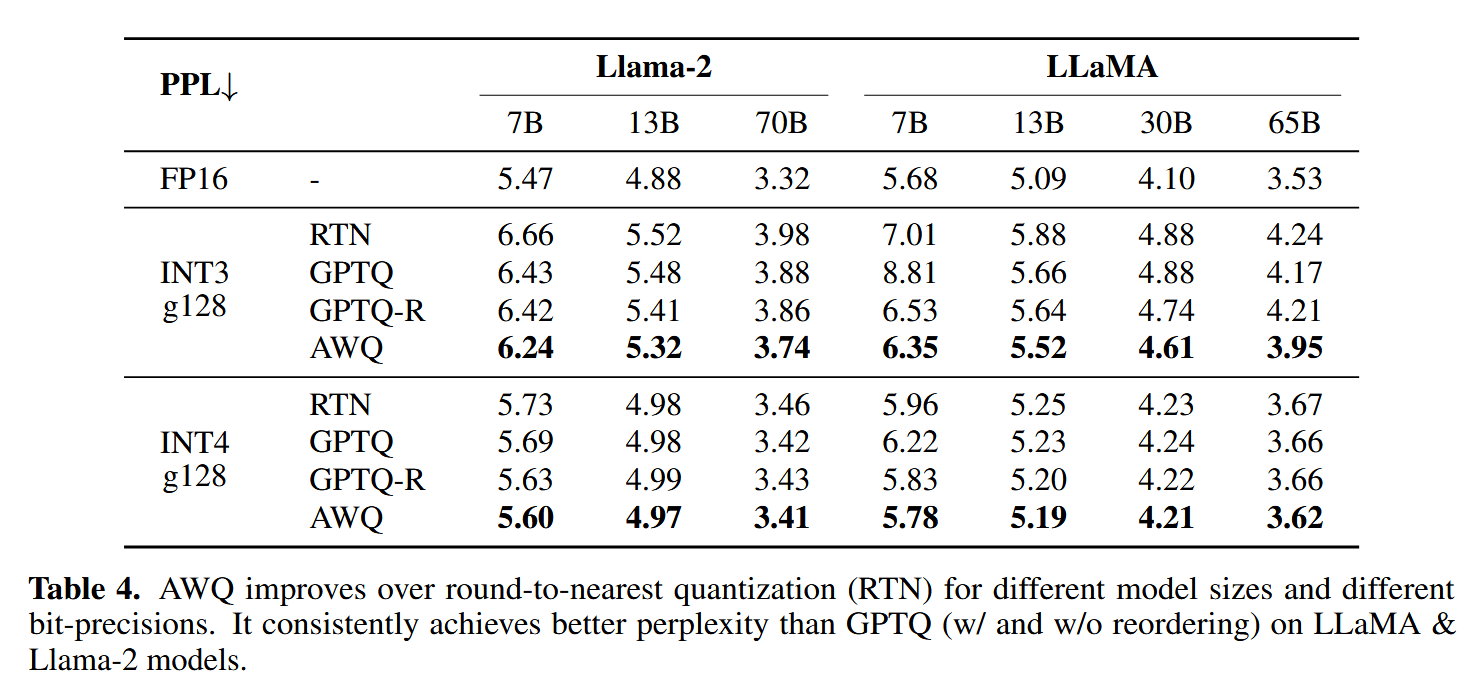
作者首先在LlaMa家族模型中进行了实验,比较在WikiText-2上的困惑度,发现AWQ的效果比GPTQ要好一点。
然后作者选取了80个样本问题,把量化前后模型的回答连接起来,让GPT-4打分判断哪个更好(交换次序后再重复一次)。结果也比之前的方法好。

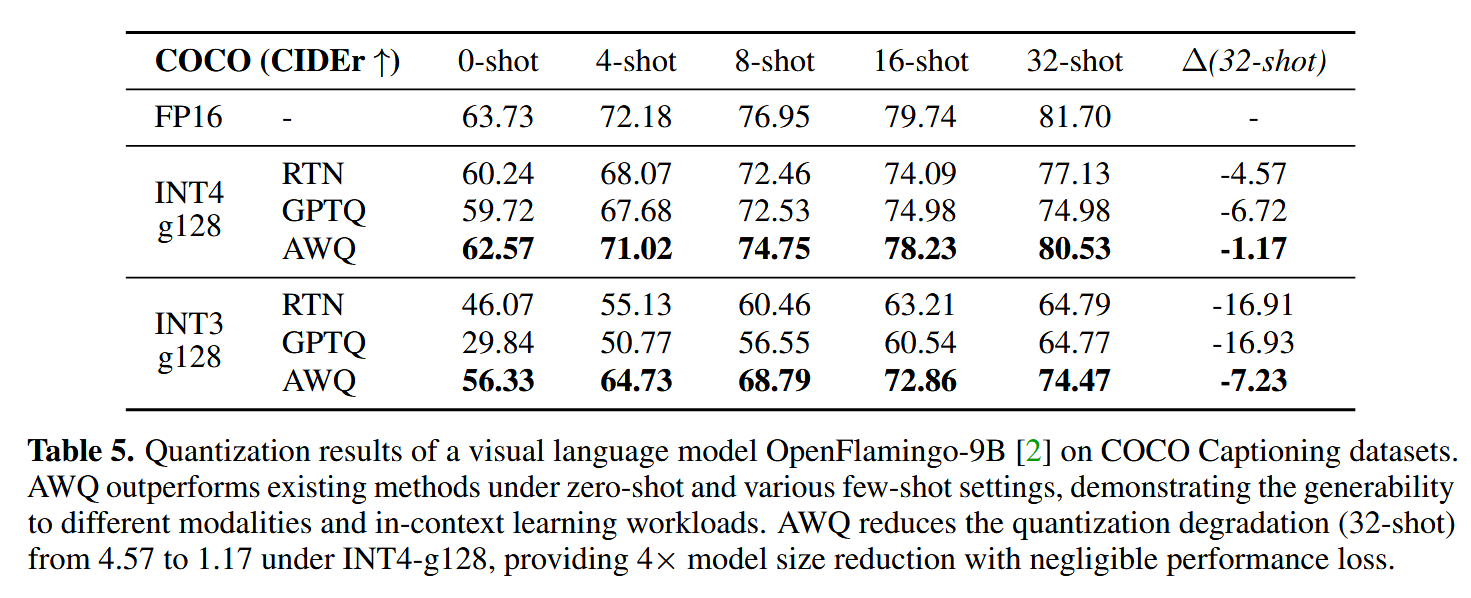
作者还测试了在多模态大模型上表现:
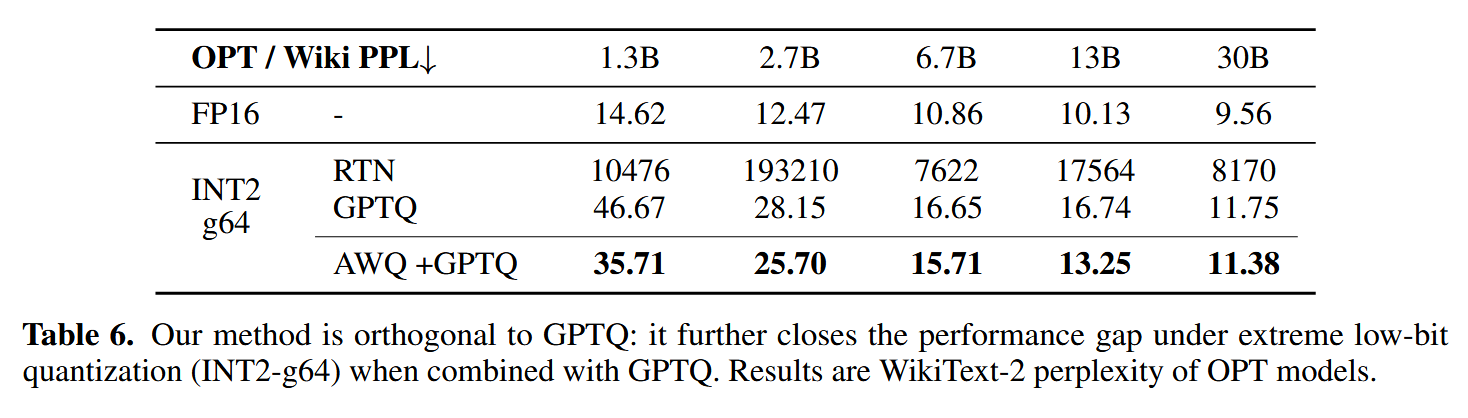
还测试了在2比特量化下的表现,作者还提出AWQ和GPTQ是可以一起使用的:
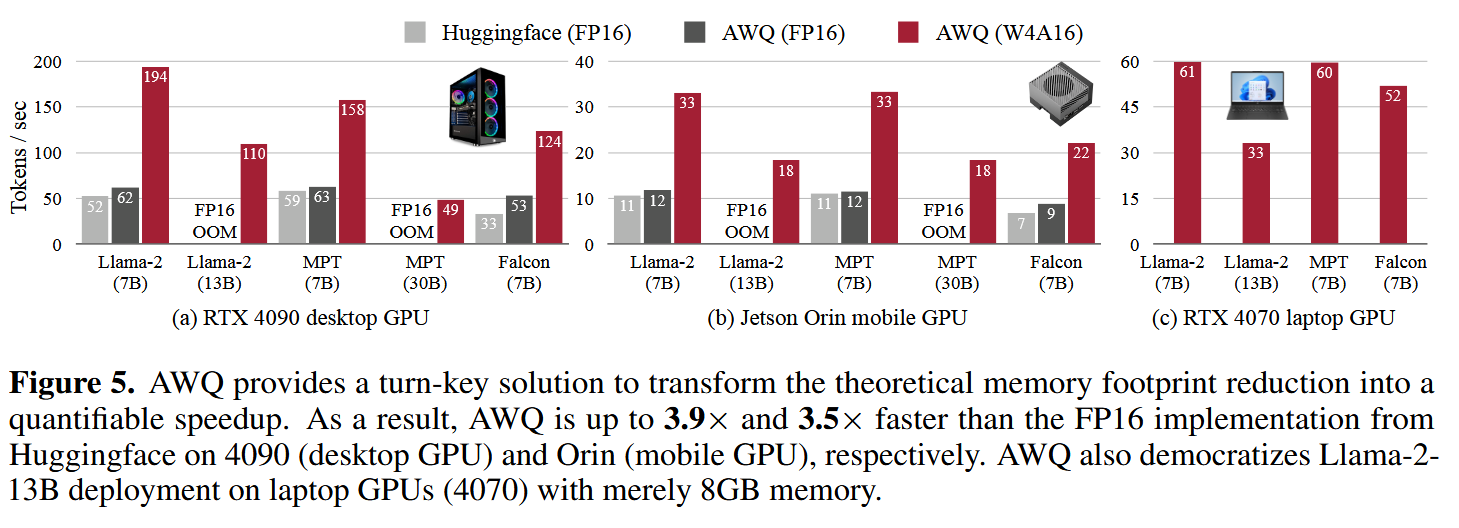
然后作者罗列了一下推理加速的效果,可以看到每秒生成的token数目增长了很多:
作者认为,由于AWQ在使用校准数据进行量化的时候没有进行反向传播,因此可以过拟合校准集合:




